How Does a Compound Symmetric Correlation Structure Translate to a Markov Model?

ordinal
prediction
regression
2023
Author
Affiliation

Frank Harrell

Department of Biostatistics
Vanderbilt University School of Medicine

Published

December 3, 2023

Random intercepts in a model induce a compound symmetric correlation structure in which the correlation between two responses on the same subject have the same correlation no matter the time gap between the responses. How does one capture such an unnatural structure using a Markov semiparametric model?

Let’s generate some data with repeatedly measured outcome per subject where the outcome is a coursened continuous response from a linear model, treated as ordinal, and the random effects have a \(N(0, 0.25^2)\) distribution. Generate 5000 subjects having 10 measurements each.

Code 
n <- 5000   # subjects
set.seed(2)
re <- rnorm(n) * 0.25
X  <- runif(n)   # baseline covariate, will be duplicated over time within subject
m  <- 10         # measurements per subject

id <- rep(1 : n, each = m)
x  <- X[id]
y  <- x + re[id] + rnorm(n * m) * 0.5
y  <- pmin(2, pmax(-1, y))   # curtail y
y  <- round(4 * y)           # coursen it
d  <- data.table(id, x, y)
d[, t := 1 : .N, by=id]
# Make short and wide dataset
w <- dcast(d[, .(id, t, y)],
           id ~ t, value.var='y')
r <- cor(as.matrix(w[, -1]), use='pairwise.complete.obs',
         method='pearson')
p <- plotCorrM(r)
p[[1]]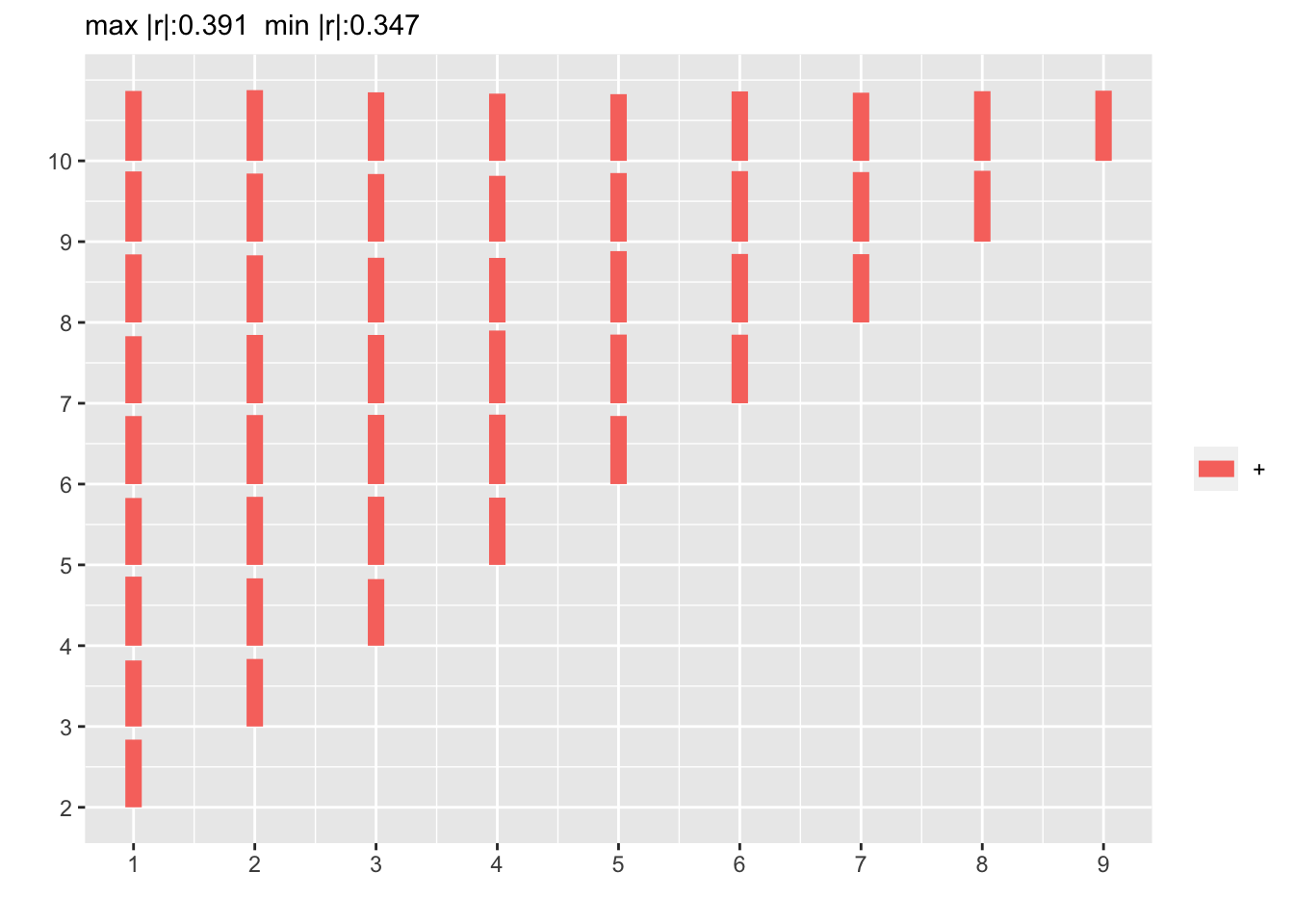

Code 
p[[2]] + ylim(0,1)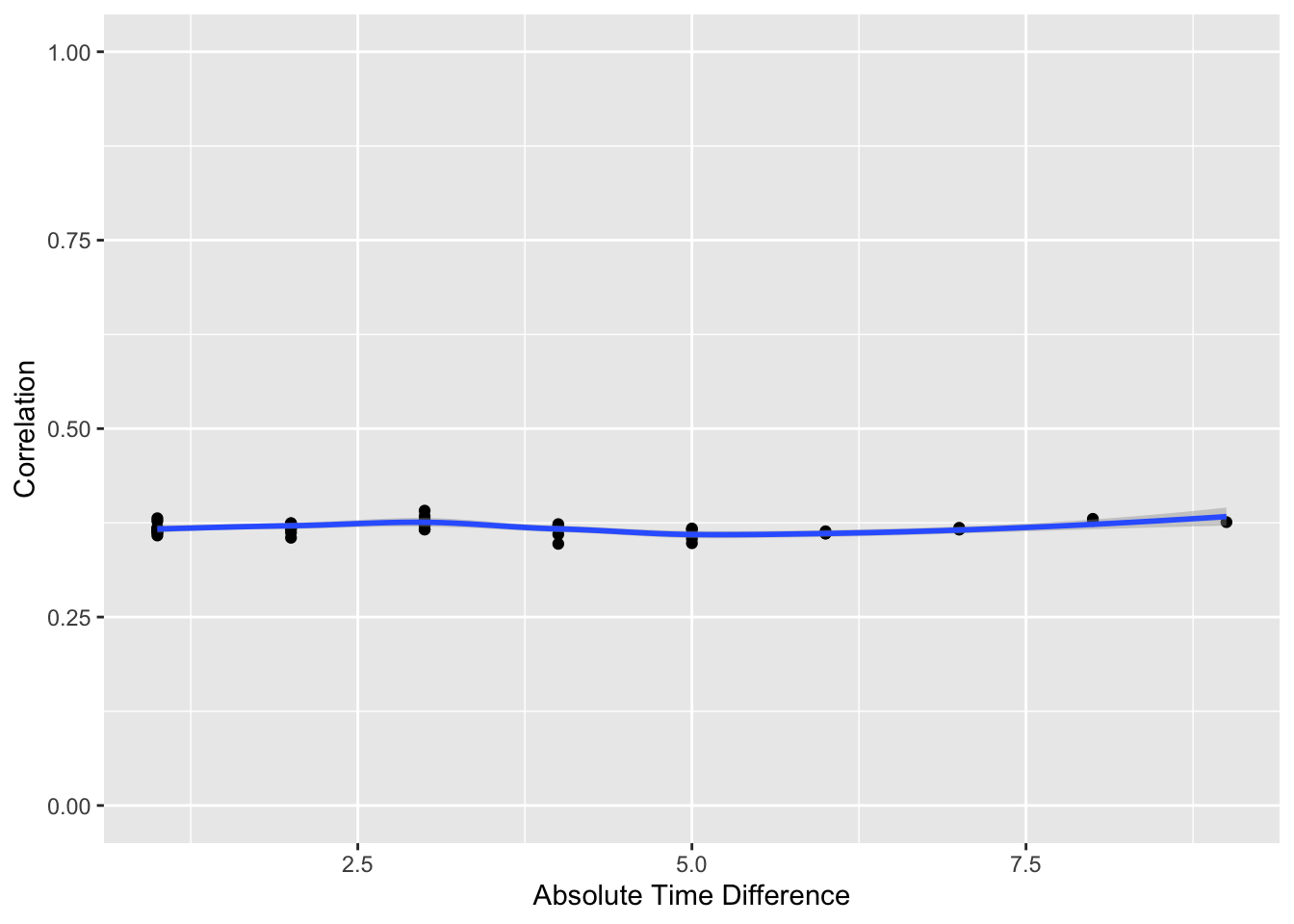

The flat correlation pattern vs. time gap is as expected.

Fit a first-order Markov PO model to times 2, 3, …, 10. Allow previous y to interact with a flexible function of time.

Code 
d[, yprev := shift(y), by=id]
f <- orm(y ~ pol(x, 2) + pol(yprev, 2) * pol(t, 3), data=d)
anova(f)
Wald Statistics for y
χ2 d.f. P
x 5565.78 2 <0.0001
 Nonlinear 6.28 1 0.0122
yprev (Factor+Higher Order Factors) 1696.29 8 <0.0001
 All Interactions 3.77 6 0.7082
 Nonlinear (Factor+Higher Order Factors) 0.68 4 0.9544
t (Factor+Higher Order Factors) 5.94 9 0.7458
 All Interactions 3.77 6 0.7082
 Nonlinear (Factor+Higher Order Factors) 2.01 6 0.9188
yprev × t (Factor+Higher Order Factors) 3.77 6 0.7082
 Nonlinear 1.50 5 0.9126
 Nonlinear Interaction : f(A,B) vs. AB 1.50 5 0.9126
 f(A,B) vs. Af(B) + Bg(A) 0.31 2 0.8560
 Nonlinear Interaction in yprev vs. Af(B) 0.43 3 0.9346
 Nonlinear Interaction in t vs. Bg(A) 1.38 4 0.8472
TOTAL NONLINEAR 8.41 9 0.4938
TOTAL NONLINEAR + INTERACTION 10.65 10 0.3853
TOTAL 11187.92 13 <0.0001
Code 
g <- orm(y ~ pol(x,2) + yprev + t, data=d)
g

Logistic (Proportional Odds) Ordinal Regression Model

orm(formula = y ~ pol(x, 2) + yprev + t, data = d)

Frequencies of Responses

  -4   -3   -2   -1    0    1    2    3    4    5    6    7    8 
 634 1012 2109 3494 5106 6413 6908 6529 5315 3620 2106 1090  664
Frequencies of Missing Values Due to Each Variable
    y     x yprev     t 
    0     0  5000     0
Model Likelihood
Ratio Test		 Discrimination
Indexes		 Rank Discrim.
Indexes
Obs 45000 LR χ2 12078.42 R2 0.238 ρ 0.488
Distinct Y 13 d.f. 4 R24,45000 0.235
Y0.5 2 Pr(>χ2) <0.0001 R24,44374.5 0.238
max |∂log L/∂β| 1×10-6 Score χ2 12153.40 |Pr(Y ≥ median)-½| 0.194
Pr(>χ2) <0.0001
β S.E. Wald Z Pr(>|Z|)
x   2.7847  0.1160 24.01 <0.0001
x2  -0.2728  0.1113 -2.45 0.0142
yprev   0.1551  0.0038 41.14 <0.0001
t   0.0040  0.0032 1.24 0.2136

There was no evidence for a nonlinear effect of previous y, or an interaction between previous value and time.

Fifth-Order Markov Model with Linear Effects

Code 
d[, yprev2 := shift(yprev),  by=id]
d[, yprev3 := shift(yprev2), by=id]
d[, yprev4 := shift(yprev3), by=id]
d[, yprev5 := shift(yprev4), by=id]
f <- orm(y ~ pol(x, 2) + yprev + yprev2 + yprev3 + yprev4 + yprev5 + t, data=d)
f

Logistic (Proportional Odds) Ordinal Regression Model

orm(formula = y ~ pol(x, 2) + yprev + yprev2 + yprev3 + yprev4 + 
    yprev5 + t, data = d)

Frequencies of Responses

  -4   -3   -2   -1    0    1    2    3    4    5    6    7    8 
 337  540 1183 1958 2754 3601 3855 3647 2964 2015 1167  622  357
image
Model Likelihood
Ratio Test		 Discrimination
Indexes		 Rank Discrim.
Indexes
Obs 25000 LR χ2 8641.08 R2 0.295 ρ 0.538
Distinct Y 13 d.f. 8 R28,25000 0.292
Y0.5 2 Pr(>χ2) <0.0001 R28,24649.9 0.295
max |∂log L/∂β| 2×10-6 Score χ2 8831.52 |Pr(Y ≥ median)-½| 0.212
Pr(>χ2) <0.0001
β S.E. Wald Z Pr(>|Z|)
x   1.6573  0.1579 10.49 <0.0001
x2  -0.2336  0.1494 -1.56 0.1180
yprev   0.0949  0.0053 17.91 <0.0001
yprev2   0.0956  0.0053 18.12 <0.0001
yprev3   0.1062  0.0053 20.07 <0.0001
yprev4   0.0882  0.0052 16.80 <0.0001
yprev5   0.0771  0.0052 14.70 <0.0001
t   0.0060  0.0079 0.76 0.4488
Code 
anova(f, yprev2, yprev3, yprev4, yprev5)
Wald Statistics for y
χ2 d.f. P
yprev2 328.18 1 <0.0001
yprev3 402.61 1 <0.0001
yprev4 282.37 1 <0.0001
yprev5 216.13 1 <0.0001
TOTAL 1833.15 4 <0.0001

For the compound symmetric correlation structure the effect of all previous values of y is the same, and all lags are important.

See if the mean of all previous values can replace all the individual lagged variables.

Code 
d[, ypmean := (yprev + yprev2 + yprev3 + yprev4 + yprev5) / 5]
fm <- orm(y ~ pol(x, 2) + ypmean + t, data=d)
fm

Logistic (Proportional Odds) Ordinal Regression Model

orm(formula = y ~ pol(x, 2) + ypmean + t, data = d)

Frequencies of Responses

  -4   -3   -2   -1    0    1    2    3    4    5    6    7    8 
 337  540 1183 1958 2754 3601 3855 3647 2964 2015 1167  622  357
Frequencies of Missing Values Due to Each Variable
     y      x ypmean      t 
     0      0  25000      0
Model Likelihood
Ratio Test		 Discrimination
Indexes		 Rank Discrim.
Indexes
Obs 25000 LR χ2 8626.32 R2 0.295 ρ 0.538
Distinct Y 13 d.f. 4 R24,25000 0.292
Y0.5 2 Pr(>χ2) <0.0001 R24,24649.9 0.295
max |∂log L/∂β| 2×10-6 Score χ2 8815.53 |Pr(Y ≥ median)-½| 0.211
Pr(>χ2) <0.0001
β S.E. Wald Z Pr(>|Z|)
x   1.6530  0.1579 10.47 <0.0001
x2  -0.2297  0.1494 -1.54 0.1243
ypmean   0.4618  0.0087 52.90 <0.0001
t   0.0061  0.0079 0.78 0.4355
Code 
AIC(fm); AIC(f)

[1] 107771.7 [1] 107765

The previous model is better but by an inconsequential amount. The compound symmetric correlation pattern is reproduced by conditioning on the mean of all previous response values.

Combined Markov and Random Effects Model

Add random intercepts and see if lags are still important in a Bayesian PO model.

Code 
require(rmsb)
options(mc.cores=4, rmsb.backend='cmdstan')  # took 7m on 4 cores (4 chains)
b <- blrm(y ~ pol(x, 2) + yprev + yprev2 + yprev3 + yprev4 + yprev5 + t +
          cluster(id), data=d, file='corstruct-b.rds')
b

Bayesian Proportional Odds Ordinal Logistic Model

Dirichlet Priors With Concentration Parameter 0.187 for Intercepts

blrm(formula = y ~ pol(x, 2) + yprev + yprev2 + yprev3 + yprev4 + 
    yprev5 + t + cluster(id), data = d, file = "corstruct-b.rds")

Frequencies of Responses

  -4   -3   -2   -1    0    1    2    3    4    5    6    7    8 
 337  540 1183 1958 2754 3601 3855 3647 2964 2015 1167  622  357
image
Mixed Calibration/
Discrimination Indexes		 Discrimination
Indexes		 Rank Discrim.
Indexes
Obs 25000 B 0.194 [0.194, 0.194] g 1.301 [1.273, 1.327] C 0.704 [0.704, 0.704]
Draws 4000 gp 0.263 [0.259, 0.267] Dxy 0.408 [0.408, 0.409]
Chains 4 EV 0.217 [0.21, 0.223]
Time 369.7s v 1.29 [1.237, 1.342]
p 8 vp 0.053 [0.051, 0.054]
Cluster on id
Clusters 5000
σγ 0.0328 [1e-04, 0.0966]
Mean β Median β S.E. Lower Upper Pr(β>0) Symmetry
x   1.6592   1.6587  0.1567   1.3281  1.9378  1.0000  0.98
x2  -0.2314  -0.2334  0.1482  -0.5081  0.0684  0.0583  1.03
yprev   0.0946   0.0946  0.0052   0.0847  0.1052  1.0000  0.99
yprev2   0.0954   0.0954  0.0051   0.0855  0.1048  1.0000  0.95
yprev3   0.1061   0.1061  0.0054   0.0955  0.1166  1.0000  1.03
yprev4   0.0883   0.0882  0.0049   0.0784  0.0977  1.0000  0.99
yprev5   0.0773   0.0773  0.0052   0.0674  0.0875  1.0000  1.01
t   0.0061   0.0061  0.0083  -0.0093  0.0228  0.7562  1.03

With the lagged variables in the model the standard deviation \(\sigma_\gamma\) of the random effects is very small, and oddly enough the previous values remain important. I conjecture that if the lagged variables were removed \(\sigma_\gamma\) would be much larger and the model would be about as good.

Computing Environment

` 
 R version 4.3.2 (2023-10-31)
 Platform: aarch64-apple-darwin20 (64-bit)
 Running under: macOS Ventura 13.6.1
 
 Matrix products: default
 BLAS:   /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRblas.0.dylib 
 LAPACK: /Library/Frameworks/R.framework/Versions/4.3-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.11.0
 
 attached base packages:
 [1] stats     graphics  grDevices utils     datasets  methods   base     
 
 other attached packages:
 [1] rmsb_1.0-0        ggplot2_3.4.4     data.table_1.14.8 rms_6.8-0        
 [5] Hmisc_5.1-2
To cite R in publications use:

R Core Team (2023). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.

To cite the Hmisc package in publications use:

Harrell Jr F (2023). Hmisc: Harrell Miscellaneous. R package version 5.1-2, https://hbiostat.org/R/Hmisc/.

To cite the rms package in publications use:

Harrell Jr FE (2023). rms: Regression Modeling Strategies. R package version 6.8-0, https://github.com/harrelfe/rms, https://hbiostat.org/R/rms/.

To cite the rmsb package in publications use:

Harrell F (2023). rmsb: Bayesian Regression Modeling Strategies. R package version 1.0-0, https://hbiostat.org/R/rmsb/.

To cite the data.table package in publications use:

Dowle M, Srinivasan A (2023). data.table: Extension of ‘data.frame’. R package version 1.14.8, https://CRAN.R-project.org/package=data.table.

To cite the ggplot2 package in publications use:

Wickham H (2016). ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York. ISBN 978-3-319-24277-4, https://ggplot2.tidyverse.org.

`{=html}