require(Hmisc)
# Load the test package for the new lrm.fit which also creates
# lrm.fit.old
require(tlrm)
# Define a function that will time a series of lines of code, repeating each
# reps times (default is 10). When only one line of code is given, the
# elapsed execution time is printed and the result of the line is returned.
# Otherwise, a vector of run times corresponding to all the lines of code is
# returned, and the values returned from the lines are stored in the global
# environment in object Res, with components named according to inputs to tim.
# When reps > 1 the values from running code lines are from the last rep.
tim <- function(...) {
reps <- 10
w <- sys.call()
n <- names(w)
m <- length(n)
k <- 2 : m
if('reps' %in% n) {
i <- which(n == 'reps')
reps <- eval(w[[i]])
k <- setdiff(k, i)
}
n <- n[k]
m <- length(n)
r <- numeric(m)
Res <<- vector('list', m) # put in global environment
names(r) <- n
names(Res) <<- n
l <- 0
for(i in k) {
l <- l + 1
s <- system.time(for(j in 1 : reps)
R <- eval(w[[i]], parent.frame()))['elapsed'] / reps
r[l] <- s
Res[[l]] <<- R
}
label(r) <- paste('Per-run execution time in seconds, averaged over', reps, 'runs')
if(m == 1) {
print(r)
return(R)
}
r
}
m <- function(x) max(abs(x))
mad <- function(a, b) c(mad = mean(abs(a - b)),
relmad = 2 * mean(abs(a - b) / (abs(a) + abs(b))))
wratio <- function(r) exp(max(abs(log(r)))) # worst ratio, whether < or > 1.0
# Function to summarize a series of model fits stored in Res
smod <- function() {
max_abs_u <- sapply(Res, function(x) if(length(x$u)) m(x$u) else NA)
iter <- sapply(Res, function(x) if(length(x$iter)) tail(x$iter, 1) else NA)
deviance <- sapply(Res, function(x) tail(x$deviance, 1))
print(data.frame(deviance, max_abs_u, iter))
l <- length(Res)
n <- names(Res)
if(l > 1) {
for(i in 1 : l) {
r <- Res[[i]]
# See if polr or BFGS
a <- inherits(r, 'polr') || (length(r$opt_method) && r$opt_method=='BFGS')
r$var <- if(inherits(r, 'orm'))
vcov(r, intercepts='all') else if(! a) vcov(r)
if(inherits(r, 'polr'))
r$coefficients <- c(-r$zeta, coef(r))
Res[[i]] <- r
}
cat('\nMaximum |difference in coefficients|,',
'Maximum |relative difference|\n',
'worst ratio of covariance matrices\n\n')
d <- NULL
for(i in 1 : (l-1))
for(j in (i+1) : l) {
ri <- Res[[i]]; rj <- Res[[j]]
comp <- paste(n[i], 'vs.', n[j])
co <- mad(ri$coefficients, rj$coefficients)
w <- data.frame(Comparison = comp,
`Max |difference|` = co[1],
`Max |rel diff|` = co[2],
`Cov ratio` = NA, check.names=FALSE)
if(length(ri$var) && length(rj$var))
w$`Cov ratio` <- wratio(ri$var / rj$var)
d <- rbind(d, w)
}
}
d$`Cov ratio` <- ifelse(is.na(d$`Cov ratio`), '', format(d$`Cov ratio`))
rownames(d) <- NULL
d
}Statistical Computing Approaches to Maximum Likelihood Estimation
computing
data-science
inference
likelihood
ordinal
prediction
r
regression
2024
Maximum likelihood estimation (MLE) is central to estimation and development of predictive models. Outside of linear models and simple estimators, MLE requires trial-and-error iterative algorithms to find the set of parameter values that maximizes the likelihood, i.e., makes the observed data most likely to have been observed under the statistical model. There are many iterative optimization algorithms and R programming paradigms to choose from. There are also many pre-processing steps to consider such as how initial parameter estimates are guessed and whether and how the design matrix of covariates is mean-centered or orthogonalized to remove collinearities. While re-writing the R
rms package logistic regression function lrm I explored several of these issues. Comparisons of execution time in R vs. Fortran are given. Different coding styles in both R and Fortran are also explored. Hopefully some of these explorations will help others who may not have studied MLE optimization and related statistical computing algorithms.
Overview
Maximum likelihood estimation (MLE) is a gold standard estimation procedure in non-Bayesian statistics, and the likelihood function is central to Bayesian statistics (even though it is not maximized in the Bayesian paradigm). MLE may be unpenalized (the standard approach) or various penalty functions such as L1 (lasso, absolute value penalty), and L2 (ridge regression; quadratic) penalties may be added to the log-likelihood to achieve shrinkage (aka regularization). I have been doing MLE my entire career, using mainly a Newton-Raphson algorithm with step-halving to achieve rapid convergence. I never stopped to think about other optimization algorithms, and the R language has a good many excellent algorithms included in the base stats package. There is also an excellent maxLik R package devoted to MLE (not used here), and two of its vignettes provide excellent introductions to MLE. General MLE background and methods including more about penalization may be found here, which includes details about how to do QR factorization and to back-transform after the fit.
If you think that ROC area or classification accuracy are good objective functions/optimality criteria, please think again.
In this article I’ll explore several optimization strategies and variations of them, in the context of binary and ordinal logistic regression. The programming scheme that is used here is the one used by many R packages: Write functions to compute the scaler objective function (here, -2 log likelihood), the gradient vector (vector of first derivatives), and the Hessian matrix (matrix of second derivatives), and pass those functions to general optimization functions. Convergence (at least to local minima for -2 LL (log of the likelihood function)) is achieved for smooth likelihood functions when the gradient vector values are all within a small tolerance (say \(10^{-7}\)) of zero or when the -2 LL objective function completely settles down in, say, the \(8^\text{th}\) significant digit. The gradient vector is all zeros if the parameter values are exactly the MLEs (local minima achieved on -2 LL).
A different strategy is to use the Bayesian system Stan by specifying LL and letting Stan analytically compute the gradient, then using the Stan optimizer to compute MLEs. If you specify priors, the optimizer provides penalized MLEs. The likelihood function is the bridge between Bayesian and frequentist methods.
History
The R rms package lrm function is dedicated to maximum likelihood estimation (MLE) for fitting binary and ordinal (proportional odds) logistic regression models using the logit link, with or without quadratic (ridge) penalization. For ordinal models, lrm is efficient for up to 400 distinct Y-values (399 intercepts) in the sense that execution time is under 10 seconds for 10,000 observations on 10 predictors. lrm uses the R function lrm.fit for its heavy lifting. Much of lrm.fit was written in 1980 and served as the computational engine for the first SAS procedure for logistic regression, PROC LOGIST. It used Fortran 77 for computationally intensive work, and used only a Newton-Raphson algorithm with step-halving for iterative MLE. On rare occasions when serious collinearities were present, such as when multiple continuous variables were fitted using restricted cubic splines (which use a truncated power basis), lrm.fit would fail to converge.
The
rms orm function is efficient for more than 8,000 intercepts. It runs in 0.45s for 400 intercepts and 10.5s for 8000 and provides the sparse covariance matrix.Re-Write of lrm.fit
To modernize the Fortran code, better condition the design matrix \(X_{n\times p}\) (\(n\) observations and \(p\) columns), and to explore a variety of optimization algorithms, I did a complete re-write of the rms package lrm and lrm.fit functions in November, 2024, for rms version 6.9-0. To reduce optimization divergence when there are extreme collinearities, and to better scale \(X\), I was interested in implementing mean centering followed by a QR factorization of \(X\) to orthogonalize its columns. Details about how this is done and how the parameter estimates and covariance matrix are converted back to the original \(X\) space may be found here. QR can be turned on by setting the lrm.fit argument transx to TRUE. When QR is in play, the rotated columns of \(X\) are scaled to have standard deviation 1.0.
rms 6.9-0 is in CRAN as of 2024-12-12. It requires an update to the Hmisc package which is already on CRAN.Besides dealing with fundamental statistical computing issues, I changed lrm.fit to use Therneau’s survival package concordancefit function to compute concordance probabilities used by various rank correlation indexes such as Somers’ \(D_{xy}\). This got rid of a good deal of code. Previously, lrm.fit binned predicted probabilities into 501 bins to calculate rank measures almost instantly. But I decided it was time to use exact calculations now that concordancefit is so fast. Though not used in rms, concordancefit also computes accurate standard errors.
A new Fortran 2018 subroutine lrmll was written to efficiently calculate the -2 log-likelihood function (the deviance), the gradient vector, and the Hessian matrix of all second partial derivatives of the log-likelihood with respect to intercept(s) \(\alpha\) and regression coefficients (slopes) \(\beta\).
lrm.fit now implements several optimization algorithms. When Y is binary and there is no penalization, it has the option to use glm.fit(..., family=binomial()) which runs iteratively reweighted least squares, a fast-converging algorithm for binary logistic regression (but does not extend to ordinal regression). lrm.fit implements 8 optimization algorithms.
- optional for proportional odds models (according to
lrm.fitinitglmargument), does a first pass withglm.fitthat fits a binary logistic regression for the probability that Y is greater than or equal to the median Y; this fit can then be used for starting values after shifting the default starting intercept values so that the middle intercept matches the intercept from the binary fit nlminb: a function in thestatspackage, tied withNRas the fastest algorithm in general; uses Hessians. This uses Fortran routines in the Bell Labs port library for which the original paper may be found here.NR: Newton-Raphson iteration with step-halving, implemented here as R functionnewtonr. This algorithm is the default because it has the advantage of having full control over convergence criteria. It requires convergence with respect to 3 simultaneous criteria: changes in -2 LL, changes in parameter estimates, and nearness of gradient to zero. The user can relax any of the 3 criteria thresholds to relax conditions. This is the optimization method used in the oldlrm.fitfunction, but written in Fortran there for slightly increased speed. Defaults for tolerance parameters are such thateps(iteration-to-iteration change in -2 LL) will usually dictate when convergence called.glm.fit: for binary Y without penalization onlynlm: thestatsfunction that is usually recommended for maximum likelihood, but I found it is slower thannlminbwithout offering other advantagesBFGSandL-BFGS-Busing thestatsoptimfunction: fast general-purpose algorithms that do not require the Hessian, so these can be used with an unlimited number of intercepts as long as the user sets thelrm.fitparametercompvartoFALSEso that the Hessian is not calculated once after convergenceCGandNelder-Mead: seeoptim
This was inspired by the
MASS package polr functionThe last four methods do not involve computing the Hessian, which is the most computationally intensive calculation in MLE. But they are still slower overall if you want to get absolute convergence, due to requiring many more evaluations of the object function (-2 LL).
See this for useful comparisons of some of the algorithms.
Background: Convergence
The two most commonly used convergence criteria for MLE are
- relative convergence: stop iterations when the change in deviance is small or when the relative change in parameter estimates is small
- absolute convergence: stop iterations when the first derivative of the log likelihood is small in absolute value for all parameters, or there is a very small absolute change in parameter values
Absolute convergence with respect to the first derivatives (gradients) is similar to demanding that none of the regression parameters change very much since the last iteration. From the standpoint of what is important statistically, convergence of the deviance (what the gold standard likelihood ratio test is based on) is sufficient with respect to what matters. Changing parameter values when the deviance does not change in the \(6^\text{th}\) decimal place will be buried in the noise. Absolute convergence may affect \(\hat{\beta}\), but relative convergence tends to result in a very stable \(\frac{\hat{\beta}}{\text{s.e.}}\). You might deem convergence satisfactory when parameter estimates between successive iterations change by less than 0.05 standard errors (which would require evaluation of the Hessian to know), but approximately this corresponds to relative convergence judged by the deviance.
Despite achieving statistically relevant convergence more easily, there is a real issue of reproducibility. Different algorithms and software may result in semi-meaningful differences in \(\hat{\beta}\) taken in isolation (ignoring how much of \(\hat{\beta}\) is noise). Only by having all the implementations achieve absolute convergence will different analysts be very likely to reproduce each others’ work. If this is important to you, either avoid the BFGS algorithms (for which the R optim function does not have an absolute convergence criterion) or use a highly stringent relative convergence criterion, e.g., specify the lrm.fit argument reltol as \(10^{-11}\). Below I explore how convergence and execution time are affected by reltol.
Overview of Findings
opt_method='NR' and 'nlminb' are the fastest methods, even slightly faster than glm.fit.
Limited tests of transx in lrm.fit to use QR factorization does not show not much benefit, but see below for details.
For ordinal Y, using opt_method='BFGS' with compvar=FALSE, compstats=FALSE mimics the polr function in the MASS package. For a large number of intercepts, lrm.fit is much faster due to computing the deviance and derivatives in highly efficient compiled Fortran, as long as the number of intercepts is less than a few hundred.
Setting initglm=TRUE tells lrm.fit to get initial ordinal model parameter values from a binary logistic glm.fit run when cutting Y at the median. This does not seem to offer much benefit over setting starting values to covariate-less MLEs of \(\alpha\) (which are calculated instantly when \(\beta=0\)) and setting \(\beta=0\). In one example using nlminb the algorithm actually diverged with initglm=TRUE but ran fine without it. This is probably due to large intercept values with many distinct Y values.
Extensive tests of opt_method='BFGS' show good stochastic performance (convergence to what matters, deviance-wise), but unimpressive execution time if you want absolute convergence by setting reltol to a small number.
The best overall algorithm that uses the Hessian is NR in terms of speed and convergence, with nlminb a close second. NR is the method used in the old lrm.fit, so for most datasets, the new optimization options are not needed.
Validation
Two kinds of validations appear below.
- Validation of the Fortran-calculated deviance and derivatives: for a given small dataset, get parameter estimates from
rms::ormwith tight convergence criteria, and test the Fortran code by evaluating the deviance and derivatives at these parameter values. The gradient (first derivative) should be very close to zero, and the deviance should be identical to that fromorm. The inverse of the negative of the Hessian matrix should equal the variance-covariance matrix computed byorm. - Validate
lrm.fitoverall by letting it pick its usual starting values for iteration, and compare its output to that fromormand other fitting functions.
Check -2 Log Likelihood and Derivatives for a Simple Model
Binary Y
x <- 1 : 10
y <- c(0, 1, 0, 0, 0, 1, 0, 1, 1, 1)
xx <- matrix(as.double(x), ncol=1)
# From orm. Deviance = 13.86294, 10.86673
alpha <- -2.4412879506377 ; beta <- 0.4438705364796
w <- .Fortran('lrmll', 10L, 1L, 1L, xx, as.integer(y), numeric(10), rep(1e0, 10), 0e0,
alpha, beta, logL=numeric(1), grad=numeric(2), numeric(0), 2L, 0L, 1L)
w$logL[1] 10.86673w$grad[1] -1.814104e-13 -1.156408e-12w <- .Fortran('lrmll', 10L, 1L, 1L, xx, as.integer(y), numeric(10), rep(1e0, 10), 0e0,
alpha, beta, logL=numeric(1), grad=numeric(2), hess=matrix(0e0, nrow=2, ncol=2), 3L, 0L, 1L)
w$hess [,1] [,2]
[1,] -1.813852 -9.976185
[2,] -9.976185 -66.123262- solve(vcov(rms::lrm(y ~ x, eps=1e-5))) Intercept x
Intercept -1.813852 -9.976185
x -9.976185 -66.123262Res <- list(glm = glm(y ~ x, family=binomial(), control=list(epsilon=1e-12)),
lrm.fit = lrm.fit(xx, y, reltol=1e-12),
old.lrm.fit = lrm.fit.old(xx, y, eps=1e-10),
orm = rms::orm(y ~ x, eps=1e-10) )
smod() deviance max_abs_u iter
glm 10.86673 NA 4
lrm.fit 10.86673 3.270271e-08 5
old.lrm.fit 10.86673 2.220446e-15 NA
orm 10.86673 NA NA
Maximum |difference in coefficients|, Maximum |relative difference|
worst ratio of covariance matrices Comparison Max |difference| Max |rel diff| Cov ratio
1 glm vs. lrm.fit 5.551115e-16 4.320309e-16 1
2 glm vs. old.lrm.fit 5.551115e-16 4.320309e-16 1
3 glm vs. orm 7.771561e-16 5.229848e-16 1
4 lrm.fit vs. old.lrm.fit 0.000000e+00 0.000000e+00 1
5 lrm.fit vs. orm 2.220446e-16 9.095388e-17 1
6 old.lrm.fit vs. orm 2.220446e-16 9.095388e-17 1# Check agreement of stats including rank correlation measures
m(Res$lrm.fit$stats - Res$old.lrm.fit$stats)[1] 3.270271e-08Cov ratio in the above output is the anti-log of the absolute value of the log of the ratio of elements of two covariance matrices. So it represents the worst disagreement in the two matrices, with 1.0 being perfect agreement to 7 decimal places. Max |difference| is the highest absolute difference in estimated regression coefficients between two methods, and Max |rel diff| is the maximum ratio of absolute differences to the sum of absolute values of two coefficient estimates.Y=0, 1, 2
x <- 1 : 10
xx <- matrix(as.double(x), ncol=1)
y <- c(0, 2, 0, 1, 0, 2, 2, 1, 1, 2)
f <- rms::orm(y ~ x, eps=1e-10) # deviance 21.77800 19.79933
- solve(vcov(f, intercepts='all')) y>=1 y>=2 x
y>=1 -2.336337 1.148893 -5.103426
y>=2 1.148893 -2.657167 -10.455125
x -5.103426 -10.455125 -110.128337- solve(vcov(rms::lrm(y ~ x, eps=1e-10))) y>=1 y>=2 x
y>=1 -2.336337 1.148893 -5.103426
y>=2 1.148893 -2.657167 -10.455125
x -5.103426 -10.455125 -110.128337- solve(vcov(MASS::polr(factor(y) ~ x))) x 0|1 1|2
x -110.12802 5.103400 10.455131
0|1 5.10340 -2.336318 1.148877
1|2 10.45513 1.148877 -2.657156# Note a problem with VGAM
- solve(vcov(VGAM::vglm(y ~ x, VGAM::cumulative(reverse=TRUE, parallel=TRUE)))) (Intercept):1 (Intercept):2 x
(Intercept):1 -2.434082 1.155134 -5.148614
(Intercept):2 1.155134 -2.580855 -9.505256
x -5.148614 -9.505256 -100.063658- solve(vcov(ordinal::clm(factor(y) ~ x))) 0|1 1|2 x
0|1 -2.336337 1.148893 5.103426
1|2 1.148893 -2.657167 10.455125
x 5.103426 10.455125 -110.128337alpha <- c(-0.8263498291155, -2.3040967379853)
beta <- 0.3091154153068
# Analytically compute 2nd derivative of log L wrt beta
info <- function(x) {
p1 <- plogis(alpha[1] + x * beta)
p2 <- plogis(alpha[2] + x * beta)
d <- p1 - p2
v1 <- p1 * (1 - p1)
v2 <- p2 * (1 - p2)
v1 - v2
w1 <- p1 * (1 - p1) * (1 - 2 * p1)
w2 <- p2 * (1 - p2) * (1 - 2 * p2)
w1 - w2
x * x * ((w1 - w2) * d - (v1 - v2)^2) / d / d
}
# Compute 2nd derivative of log(p1 - p2) wrt beta numerically
dif <- function(x, beta) log(plogis(alpha[1] + x * beta) - plogis(alpha[2] + x * beta))
del = 1e-6
d2 <- function(x) ((dif(x, beta + del) - dif(x, beta)) / del - (dif(x, beta) - dif(x, beta - del)) / del) / del
c(info(4), info(8), info(9))[1] -6.88269 -24.55641 -27.93077num <- c(d2(4), d2(8), d2(9))
print(num)[1] -6.882495 -24.556135 -27.931213sum(num)[1] -59.36984w <- .Fortran('lrmll', 10L, 2L, 1L, xx, as.integer(y), numeric(10), rep(1e0, 10), 0e0,
alpha, beta, logL=numeric(1), grad=numeric(3), numeric(0), 2L, 0L, 1L)
w$logL[1] 19.79933w$grad[1] -1.896261e-13 -1.408873e-13 -2.330580e-12w <- .Fortran('lrmll', 10L, 2L, 1L, xx, as.integer(y), numeric(10), rep(1e0, 10), 0e0,
alpha, beta, logL=numeric(1), grad=numeric(3), hess=matrix(0e0, nrow=3, ncol=3), 3L, 0L, 1L)
w$hess [,1] [,2] [,3]
[1,] -2.336337 1.148893 -5.103426
[2,] 1.148893 -2.657167 -10.455125
[3,] -5.103426 -10.455125 -110.128337Simple Ordinal Model With Weights, Offsets, and Penalties
We first ignore weights, offsets, and penalties, then incorporate them.
set.seed(1)
x1 <- rnorm(50)
x2 <- rnorm(50)
X <- cbind(x1, x2)
y <- sample(0:5, 50, TRUE)
wt <- runif(50)
wt <- wt / sum(wt)
of <- rnorm(50)
pm <- cbind(c(1.2, 0.6), c(0.6, 1.2))
f <- lrm.fit.old(X, y, eps=1e-15) # (y ~ x1 + x2, eps=1e-15)
f$deviance[1] 177.1350 176.8656cof <- coef(f)
w <- .Fortran('lrmll', 50L, 5L, 2L, X, as.integer(y), rep(0e0, 50),
rep(1e0, 50), 0 * pm,
cof[1:5], cof[6:7], logL=numeric(1), grad=numeric(7), numeric(0),
2L, 0L, 0L)
w$logL[1] 176.8656w$grad[1] 3.330669e-16 3.552714e-15 2.886580e-15 -2.886580e-15 1.998401e-15
[6] 1.998401e-15 1.332268e-15w <- .Fortran('lrmll', 50L, 5L, 2L, X, as.integer(y), rep(0e0, 50),
rep(1e0, 50), 0 * pm,
cof[1:5], cof[6:7], logL=numeric(1), grad=numeric(7),
hess=matrix(0e0, nrow=7, ncol=7),
3L, 0L, 0L)
range(w$hess + solve(vcov(f)))[1] -1.421085e-14 1.065814e-14# Needed reltol=1e-15 to get gradient to 1e-8 with BFGS
# CG achieved 1e-6 with default, with 475 function evaluations
g <- lrm.fit(X, y, trace=1, opt_method='nlm', gradtol=1e-14,
transx=TRUE, compstats=FALSE)iteration = 0
Step:
[1] 0 0 0 0 0 0 0
Parameter:
[1] 1.51634749 0.57536414 -0.08004271 -0.84729786 -2.19722458 0.00000000
[7] 0.00000000
Function Value
[1] 177.135
Gradient:
[1] 1.199041e-14 -2.664535e-15 -1.243450e-14 7.993606e-15 3.330669e-15
[6] 2.510851e+00 3.400018e+00
iteration = 4
Parameter:
[1] 1.53972787 0.60066749 -0.06107634 -0.83760533 -2.19876783 -0.07124309
[7] -0.10606549
Function Value
[1] 176.8656
Gradient:
[1] -8.388246e-11 -3.561773e-11 8.475087e-11 1.565637e-11 7.530643e-13
[6] 5.342615e-12 9.455770e-13
Last global step failed to locate a point lower than x.
Either x is an approximate local minimum of the function,
the function is too non-linear for this algorithm,
or steptol is too large.m(g$u); g$iter # L-BFGS-B tool factor as low as 1e2 to get u=3e-6, 50 iter[1] 4.237544e-11[1] 4mad(cof, g$coefficients) mad relmad
1.377462e-12 4.676386e-12 range(f$var / g$var)[1] 1 1Now use weights, offset, and penalties.
f <- rms::lrm(y ~ x1 + x2 + offset(of), weights=wt, penalty=2,
penalty.matrix=pm, eps=1e-12)
f$deviance[1] 3.475801 3.803296 3.799336cof <- coef(f)
w <- .Fortran('lrmll', 50L, 5L, 2L, cbind(x1, x2), as.integer(y), of, wt,
2e0 * pm,
cof[1:5], cof[6:7], logL=numeric(1), grad=numeric(7), numeric(0),
2L, 0L, 1L)
w$logL[1] 3.799336w$grad[1] 8.500145e-17 4.163336e-17 -1.370432e-16 2.775558e-17 -1.994932e-17
[6] 5.898060e-17 1.387779e-17w <- .Fortran('lrmll', 50L, 5L, 2L, cbind(x1, x2), as.integer(y), of, wt,
2 * pm,
cof[1:5], cof[6:7], logL=numeric(1), grad=numeric(7),
hess=matrix(0e0, nrow=7, ncol=7),
3L, 0L, 1L)
range(w$hess + solve(vcov(f)))[1] -2.775558e-16 1.332268e-15g <- lrm.fit(cbind(x1, x2), y, trace=3, offset=of, weights=wt,
penalty.matrix=2e0*pm, opt_method='nlminb', compstats=FALSE) 0: 3.8301785: 1.23911 0.611204 -0.0435624 -0.772679 -2.45652
3: 3.8032957: 1.50965 0.925273 0.280639 -0.513375 -2.39790
0: 3.8032957: 1.50965 0.925273 0.280639 -0.513375 -2.39790 0.00000 0.00000
3: 3.7993356: 1.50984 0.927634 0.283085 -0.513316 -2.39750 0.0149656 -0.0431891m(g$u); g$iter[1] 3.404934e-09 iterations evaluations.function evaluations.gradient
3 4 3 mad(coef(f), coef(g)) mad relmad
7.703453e-09 7.127106e-09 g$iter iterations evaluations.function evaluations.gradient
3 4 3 g$u y>=1 y>=2 y>=3 y>=4 y>=5
3.404934e-09 6.040723e-10 -1.193834e-09 -1.123210e-09 -1.671228e-09
x1 x2
3.391934e-10 7.970911e-11 f$deviance[1] 3.475801 3.803296 3.799336g$deviance[1] 3.475801 3.803296 3.799336range(f$var / g$var)[1] 0.9999999 1.0000002Check Accuracy Against Old lrm.fit For a Variety of Levels of Y
set.seed(1)
n <- 150
w <- NULL
for(i in 1 : 40) {
k <- sample(1 : 20, 1, TRUE)
y <- sample(0 : k, n, TRUE)
x1 <- runif(n)
x2 <- exp(rnorm(n))
X <- cbind(x1, x2)
f <- lrm.fit.old(X, y, eps=1e-10)
g <- lrm.fit( X, y, opt_method='nlminb', compstats=FALSE)
d <- coef(f) - coef(g)
r <- wratio(vcov(f) / vcov(g))
w <- rbind(w, data.frame(i, k, mad.beta=m(d), Cov.ratio=r))
}
range(w$Cov.ratio)[1] 1 1with(w, plot(k, mad.beta, log='y'))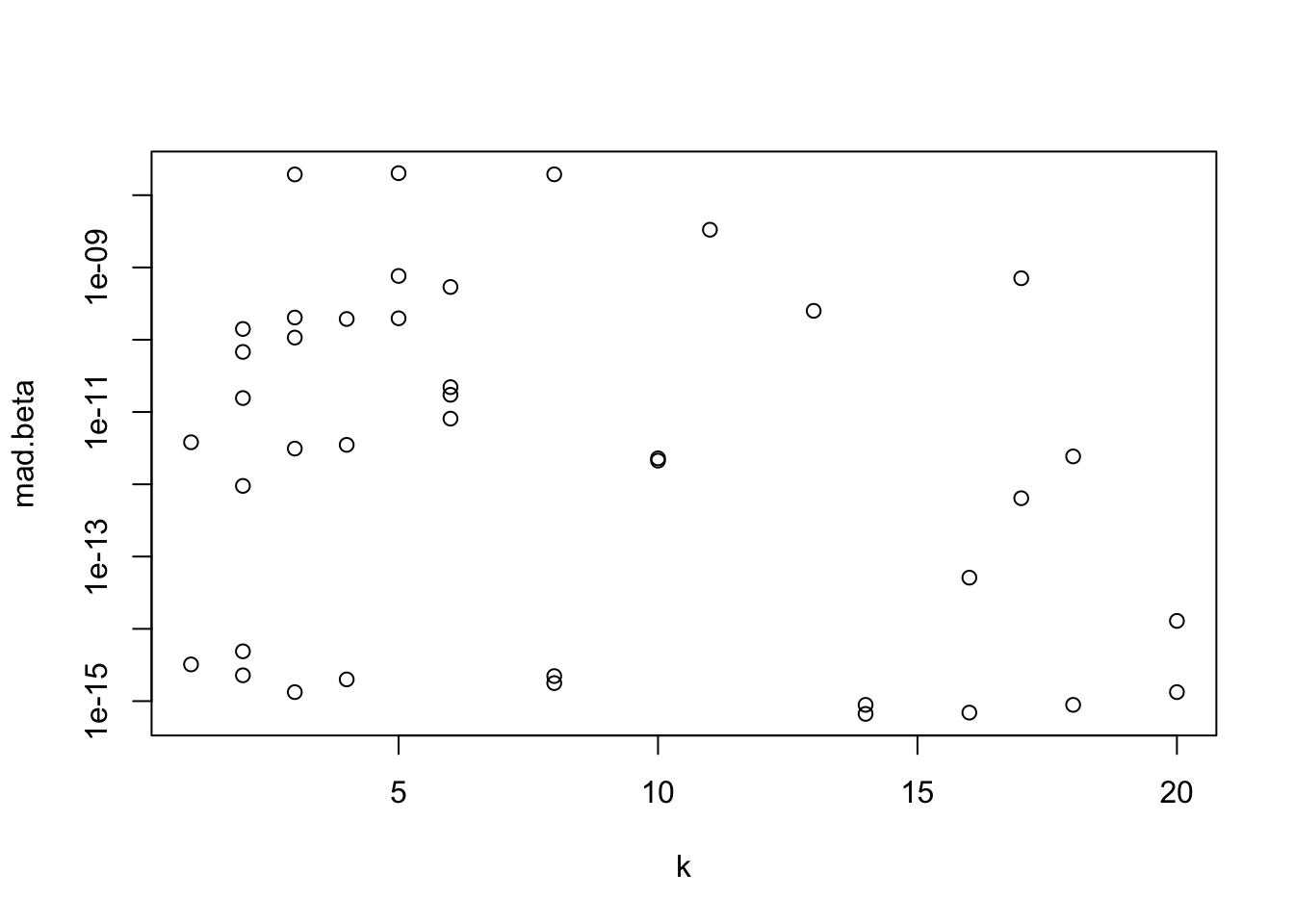
Study Convergence and Timings
Fortran vs. R
Regarding execution speed, a key question is whether it’s worth the effort to code part of the calculations in a compiled language such as Fortran, C, or C++, as compared to just using R. Let’s explore this by coding the gradient vector calculation in R and timing it against the new Fortran code. Also write a function making the Fortran routine easy to call when computing the gradient.
The code below makes use of the facts that \(\frac{\partial \log \text{expit}(x)}{\partial x} = \text{expit}(-x) = 1 - \text{expit}(x)\) and \(\frac{\partial \text{expit}(x)}{\partial x} = \text{expit(x)}(1 - \text{expit(x)})\). The philosophy of this code is that nothing is calculated unless it is relevant, which makes for more lines of code. For example, the code does not create extra intercepts to yield probabilities of 0 or 1, but instead handles each case Y=0, Y=\(k\), \(0 < \text{Y} < k\) separately. For the non-interior levels of Y the gradient is very simple as probabilities are expits and not differences.
grad <- function(alpha, beta, x, y) {
k <- length(alpha)
p <- length(beta)
f <- plogis
xb <- as.vector(x %*% matrix(beta, nrow=p))
xb <- as.vector(x %*% beta)
P1 <- P2 <- numeric(n)
i0 <- y == 0
ik <- y == k
ib <- y > 0 & y < k
P1[i0] <- 1e0
P2[i0] <- f(alpha[1] + xb[i0])
P1[ik] <- f(alpha[k] + xb[ik])
P2[ik] <- 0e0
P1[ib] <- f(alpha[y[ib] ] + xb[ib])
P2[ib] <- f(alpha[y[ib] + 1] + xb[ib])
pq1 <- P1 * (1e0 - P1)
pq2 <- P2 * (1e0 - P2)
P <- P1 - P2
U <- rep(0e0, k + p)
U[1] <- - sum(1e0 - P[i0])
U[k] <- U[k] + sum(1e0 - P[ik])
# Gradiant for intercepts
if(k > 1) for(m in 1 : k) { # only interior y values create complexity
if(m < k) U[m] <- U[m] + sum(pq1[y == m] / P[y == m])
if(m > 1) U[m] <- U[m] - sum(pq2[y == m - 1] / P[y == m - 1])
}
# Gradient for slopes
for(m in 1 : p) {
U[k + m] <- - sum(x[i0, m] * (1e0 - P[i0]))
U[k + m] <- U[k + m] + sum(x[ik, m] * (1e0 - P[ik]))
if(k > 1) for(i in 1 : (k - 1)) {
j <- y == i
U[k + m] <- U[k + m] + sum(x[j, m] * (pq1[j] - pq2[j]) / P[j])
}
}
U
}
fgrad <- function(alpha, beta, x, y) {
x <- as.matrix(x)
n <- nrow(x)
p <- ncol(x)
k <- max(y) # y assumed to be coded 0-k
.Fortran('lrmll',
as.integer(n), as.integer(k), as.integer(p),
x, y, rep(0e0, n), rep(1e0, n), matrix(0e0, nrow=p, ncol=p),
alpha, beta, numeric(1), u=numeric(k + p), numeric(1), 2L, 0L, 0L)$u
}
# This calls a version of the Fortran code using the alpha extension approach
fgrad2 <- function(alpha, beta, x, y) {
x <- as.matrix(x)
n <- nrow(x)
p <- ncol(x)
k <- max(y) # y assumed to be coded 0-k
.Fortran('lrmll2',
as.integer(n), as.integer(k), as.integer(p),
x, y, rep(0e0, n), rep(1e0, n), matrix(0e0, nrow=p, ncol=p),
alpha, beta, numeric(1), u=numeric(k + p), numeric(1), 2L, 0L, 0L)$u
}But is the elegance of following the letter of the proportional odds model’s definition worth the trouble? What if we used the trick that is most often used in MLE and Bayesian modeling where we define extra intercepts so that all values of Y appear to be interior values and the same difference in probabilities can be computed everywhere, and we did not use special cases to compute derivatives of log likelihood components? Specifically we can write the model as the following, with y = \(0, 1, \ldots, k\) and \(\text{expit}(x) = \frac{1}{1 + \exp(-x)}\).
\[\Pr(Y \geq y) = \text{expit}(\alpha_y + X\beta)\]
by expanding the original vector of intercepts \(\alpha\) by adding \(\alpha_0 = 100\) and \(\alpha_{k+1} = -100\). Then \(\Pr(Y = y) = \text{expit}(\alpha_y + X\beta) - \text{expit}(\alpha_{y+1} + X\beta)\) for any \(y=0, \ldots, k\). The \(\pm 100\) is chosen so that \(\text{expit}(x)\) is indistinguishable from 1 and 0.
We need to run some computational tests to make sure that the upcoming shortcuts do not cause any computational inefficiencies or inaccuracies.
# Check that R computes expit very quickly for extreme values of x
tim(smallvals = plogis(rep( 1, 100000)),
m50 = plogis(rep(-50, 100000)),
p50 = plogis(rep( 50, 100000)))Per-run execution time in seconds, averaged over 10 runs
smallvals m50 p50
0.0011 0.0010 0.0011 # Check that taking the log of probabilities is as accurate as
# using plogis' special log probability calculation
x <- seq(-50, 50, by=1); m(log(plogis(x)) - plogis(x, log=TRUE))[1] 8.881784e-16So it appears that the “intercept extension” approach will not cause any numerical problems. To code this method while computing the gradient, we need the derivative of the log of the difference in probabilities (call this \(Q = P_1 - P_2\)) given above. Consider a general parameter \(\theta\) which may be one of the (interior) \(\alpha\)s or one of the \(\beta\)s.
\[\frac{\partial \log(Q)}{\partial\theta} = \frac{\frac{\partial P_1}{\partial\theta} - \frac{\partial P_2}{\partial\theta}}{Q}\] Since the main part of \(\frac{\partial \text{expit}(x)}{\partial\theta} = \text{expit(x)}(1 - \text{expit(x)})\),
\[\frac{\partial P_1}{\partial\theta} = P_1 (1 - P_1) \frac{\partial(\alpha_y + X\beta)}{\partial\theta}\] \[\frac{\partial P_2}{\partial\theta} = P_2 (1 - P_2) \frac{\partial(\alpha_{y + 1} + X\beta)}{\partial\theta}\]
\(\frac{\partial(\alpha_{y} + X\beta)}{\partial\theta}\) is the 0/1 indicator function \([y=j]\) when \(\theta = \alpha_{j}\) and is \(X_{j}\) when \(\theta = \beta_{j}\). Now code this in R.
grad2 <- function(alpha, beta, x, y) {
k <- length(alpha)
p <- length(beta)
xb <- as.vector(x %*% matrix(beta, nrow=p))
xb <- as.vector(x %*% beta)
alpha <- c(100e0, alpha, -100e0)
# Must add 1 to y to compute P1 and P2 since index starts at 1, not 0
P1 <- plogis(alpha[y + 1] + xb)
P2 <- plogis(alpha[y + 2] + xb)
Q <- P1 - P2
pq1 <- P1 * (1e0 - P1)
pq2 <- P2 * (1e0 - P2)
U <- numeric(k + p)
# Gradiant for intercepts
for(m in 1 : k)
U[m] <- sum((pq1 * (y == m) - pq2 * (y + 1 == m)) / Q)
# Use element-wise multiplication then get the sum for each column
# Element-wise = apply the same value of the weights to each row of x
U[(k + 1) : (k + p)] <- colSums(x * (pq1 - pq2) / Q)
U
}Check that grad and grad2 yield the same answer and check their relative speeds.
set.seed(1)
n <- 50000; p <- 50; k <- 100
x <- matrix(rnorm(n * p), nrow=n)
y <- sample(0 : k, n, TRUE)
stopifnot(length(unique(y)) == k + 1)
alpha <- seq(-6, 6, length=k)
beta <- runif(p, -0.5, 0.5)
tim(g1 = grad( alpha, beta, x, y),
g2 = grad2(alpha, beta, x, y),
reps = 5) # creates ResPer-run execution time in seconds, averaged over 5 runs
g1 g2
1.013 0.076 m(Res$g1 - Res$g2) # maximum absolute difference[1] 4.774847e-11Even though the streamlined code in grad2 required evaluating a few quantities that are known to be 0 or 1, its vectorization resulted in significantly faster R code. Later this will be compared with the speed of Fortran code.
Fortran Code for Gradient
Here is the central part of the Fortran code for computing the gradient vector. Fortran is blazing fast and easier to learn than C and C++, so more users may wish to translate some execution-time critical portions of their R code to Fortran 2018. R makes it easy to include Fortran code in packages, and it is also easy to include Fortran functions in RStudio sessions.
u = 0_dp
! All obs with y=0
! The derivative of log expit(x) wrt x is expit(-x)
! Prob element is expit(-alpha(1) - lp)
u(1) = - sum(wt(i0) * (1_dp - d(i0)))
if(p > 0) then
do l = 1, p
u(k + l) = - sum(wt(i0) * x(i0, l) * (1_dp - d(i0)))
end do
end if
! All obs with y=k
! Prob element is expit(alpha(k) + lp)
u(k) = u(k) + sum(wt(ik) * (1_dp - d(ik)))
if(p > 0) then
do l = 1, p
u(k + l) = u(k + l) + sum(wt(ik) * x(ik, l) * (1_dp - d(ik)))
end do
end if
! All obs with 0 < y < k
if(nb > 0) then
do ii = 1, nb
i = ib(ii)
j = y(i)
! For p1, D() = 1 for alpha(j), 0 for alpha(j+1)
! For p2, D() = 0 for alpha(j), 1 for alpha(j+1)
u(j) = u(j) + wt(i) * v1(i) / d(i)
u(j + 1) = u(j + 1) - wt(i) * v2(i) / d(i)
if(p > 0) then
do l = 1, p
u(k + l) = u(k + l) + wt(i) * x(i, l) * (v1(i) - v2(i)) / d(i)
end do
end if
end doThis code can be streamlined using the \(\alpha\) extension approach:
ealpha = [100d0, alpha, -100d0]
p1 = expit(ealpha(y + 1) + lp)
p2 = expit(ealpha(y + 2) + lp)
q = p1 - p2
pq1 = p1 * (1_dp - p1)
pq2 = p2 * (1_dp - p2)
do j = 1, k
u(j) = sum((pq1 * merge(1_dp, 0_dp, y == j) - &
pq2 * merge(1_dp, 0_dp, y + 1 == j)) / (q / wt))
end do
if(p > 0) then
do j = 1, p
u(k + j) = sum(x(:, j) * (pq1 - pq2) / (q / wt))
end do
end ifBut this code runs faster (this is the code tested below):
do i = 1, n
w = q(i) / wt(i)
do j = 1, k
if(y(i) == j) u(j) = u(j) + pq1(i) / w
if(y(i) + 1 == j) u(j) = u(j) - pq2(i) / w
end do
if(p > 0) then
do j = 1, p
u(k + j) = u(k + j) + x(i, j) * (pq1(i) - pq2(i)) / w
end do
end if
end doFirst let’s compare accuracy and speed of two ways of coding the gradient calculation in Fortran (click above to see both versions).
tim(Fortran = fgrad (alpha, beta, x, y),
Fortran2 = fgrad2(alpha, beta, x, y), reps=40 )Per-run execution time in seconds, averaged over 40 runs
Fortran Fortran2
0.0090 0.0127 m(Res$Fortran - Res$Fortran2)[1] 6.82121e-12Though it produces the same result to within \(7\times 10^{-12}\), the streamlined Fortran is \(1.5\times\) slower than the longer Fortran code.
Run the R grad2 function defined above, and the Fortran routine included in the new rms package, for \(n=50,000\), \(p=50\) predictors, and \(k=100\) intercepts.
# Check agreement of R and Fortran code
tim(R = grad2(alpha, beta, x, y),
Fortran = fgrad(alpha, beta, x, y), reps=40 )Per-run execution time in seconds, averaged over 40 runs
R Fortran
0.061975 0.008750 m(Res$R - Res$Fortran)[1] 6.82121e-12We see that the compiled Fortran code is \(> 7\times\) faster than the R code. In a nutshell Fortran allows you to not worry about vectorizing calculations, allowing for simpler code (there are many functions in Fortran for vectorizing operations but these are used more for brevity than for speed).
A more vectorized version of the code, written by ChatGPT, gave completely incorrect results but only ran faster by a ratio of 0.84. After much prompting, ChatGPT could only get the right answer if it re-wrote the code to be very inefficient by using excessive loops.
ChatGPT’s Compact But Non-Working Code
As streamlined as this code is, it does not improve execution time over my R grad function, taking 1.1s to run on the data given above while yielding the wrong answer.
gradient_proportional_odds <- function(alpha, beta, X, Y) {
n <- nrow(X) # Number of observations
p <- ncol(X) # Number of predictors
k <- length(alpha) # Number of thresholds (max Y value)
# Compute linear predictors
eta <- X %*% beta # n x 1 vector
# Expand eta to match dimensions with alpha
eta_matrix <- matrix(eta, n, k, byrow = FALSE) # n x k matrix
# Compute expit(alpha_y + eta) for all thresholds y
eta_alpha <- eta_matrix + matrix(alpha, n, k, byrow = TRUE)
expit_vals <- 1 / (1 + exp(-eta_alpha)) # n x k matrix of expit values
# Compute probabilities for P(Y = y)
expit_upper <- cbind(1, expit_vals) # P(Y >= 0) = 1
expit_lower <- cbind(expit_vals, 0) # P(Y >= k+1) = 0
prob_Y <- expit_upper[, 1:k] - expit_lower[, 1:k] # P(Y = y)
# Indicator matrix for observed Y
Y_ind <- matrix(0, n, k)
for (i in 1:k) Y_ind[, i] <- as.numeric(Y == (i - 1))
# Compute weights (observed minus predicted probabilities)
weights <- (Y_ind - prob_Y)
# Gradients w.r.t. alpha
grad_alpha <- colSums(weights)
# Gradients w.r.t. beta
d_expit <- expit_vals * (1 - expit_vals) # Derivative of expit
grad_beta <- numeric(p)
for (j in 1:p) {
grad_beta[j] <- sum(weights * d_expit * X[, j])
}
# Combine gradients
grad <- c(grad_alpha, grad_beta)
return(grad)
}The Hessian requires about a factor of \(\frac{k + p}{2}\) more calculations than the gradient when computed inefficiently, so the Fortran code pays off even more when using Hessian-based optimization algorithms or computing the final covariance matrix. The lrmll Fortran code called by the new lrm.fit creates a large Hessian matrix when \(k\) is large, because it does not store the result as a sparse (tri-band diagonal) matrix. It is very computationally efficient though, because in computing the Hessian it does not add any terms that are zero. So computationally, it capitalizes on the tri-band diagonal form of the Hessian for the cumulative probability model. Until the Hessian needs to be inverted, lrmll is even more efficient than the code in orm.fit because more of the code in lrmll is written in Fortran, and the Fortran code is a little more efficient than the Fortran with orm.fit. In rms 6.9-1 expected to be on CRAN in early 2025, orm.fit was completely re-written to benefit from Fortran code like what lrm.fit uses, and to use the Matrix package for more efficient sparse matrix handling.
Efficient Computation of the Hessian for General Cumulative Probability Models
The lrmll Fortran subroutine computes the Hessian very efficiently for the proportional odds model (logit link), making use of simplifications for the logistic model. Now consider general links. For \(Y = 1, ..., k - 1, P(Y = j)\) is written in terms of the cumulative probability function \(f\) by \(f(\alpha_{j} + X\beta) - f(\alpha_{j+1} + X\beta)\). We need all the second partial derivatives of the log of this difference in cumulative probabilities. Let’s simplify the expression to \(f(a + \beta x) - f(b + \beta x)\). ChatGPT provided the following results, which I simplified somewhat and corrected a sign error in \(\frac{\partial^2 g}{\partial b \ \partial \beta}\).
- Let \(g(a, b, \beta, x) = \log\left(f(a + \beta x) - f(b + \beta x)\right)\)
- Let \(F(a, b, \beta, x) = f(a + \beta x) - f(b + \beta x)\)
- Substitute \(d\) for \(F(a, b, \beta, x)\) post differentiation
- Divide all the second partial derivatives below by \(d^2\)
\[ \begin{aligned} \frac{\partial^2 g}{\partial a^2} &= d f''(a + \beta x) - f'(a + \beta x)^2 \\ \frac{\partial^2 g}{\partial b^2} &= -d f''(b + \beta x) - f'(b + \beta x)^2 \\ \frac{\partial^2 g}{\partial \beta^2} &= x^2 d \big(f''(a + \beta x) - f''(b + \beta x)\big) - x^{2} \big(f'(a + \beta x) - f'(b + \beta x)\big)^2 \\ \frac{\partial^2 g}{\partial a \partial b} &= f'(a + \beta x) \cdot f'(b + \beta x) \\ \frac{\partial^2 g}{\partial a \partial \beta} &= x d f''(a + \beta x) - x f'(a + \beta x) \cdot \big(f'(a + \beta x) - f'(b + \beta x)\big) \\ \frac{\partial^2 g}{\partial b \partial \beta} &= -x d f''(b + \beta x) + x f'(b + \beta x) \cdot \big(f'(a + \beta x) - f'(b + \beta x)\big) \end{aligned} \]
For derivatives with respect only to \(\beta\), substitute \(x_{i} x_{j}\) for \(x^2\) to get second partial derivatives with respect to \(\beta_{i}\) and \(\beta_{j}\).
Let \(d = 1 - f\) for \(Y=0\) and \(d = f\) otherwise. For the interior values of \(Y\), first consider \(Y=0\) which has probability \(d = 1 - f(a + x \beta)\). The second partial derivatives are, when multiplied by \((1 - f)^{2} = d^{2}\),
\[ \begin{aligned} \frac{\partial^2 g}{\partial a^2} &= - f'^{2} - df'' \\ \frac{\partial^2 g}{\partial \beta^2} &= - x^{2} \big(f'^{2} + df''\big) \\ \frac{\partial^2 g}{\partial a\partial\beta} &= - x\big(f'^{2} - df''\big) \end{aligned} \]
Here \(f\) stands for \(f(a + \beta x)\) etc.
For \(Y=k\) the Hessian elements are, when multiplied by \(f^2\),
\[ \begin{aligned} \frac{\partial^2 g}{\partial a^2} &= d f'' - f'^{2} \\ \frac{\partial^2 g}{\partial \beta^2} &= x^{2} \big(d f'' - f'^{2}\big) \\ \frac{\partial^2 g}{\partial a\partial\beta} &= x\big(d f'' - f'^{2}\big) \end{aligned} \]
All these formulas are implemented in the ormll Fortran subroutine used in the 6.9-1 version of rms.
Use of Jacobians to Translate Hessian on One Scale To Another Scale
Sometimes it’s easier to derive second derivatives on the original scale without logging, and using a Jacobian to translate to the other scale. ChatGPT provided the following Jacobian solution for our example. This is not used in the Fortran code because it might slow it down a bit. I believe that MASS::polr uses the Jacobian approach.
To systematically compute and represent the transformation of the second partial derivatives of \(F(a, b, \beta, x)\) into the second partial derivatives of \(g(a, b, \beta, x) = \log(F(a, b, \beta, x))\), we organize the derivatives into a Hessian matrix and apply the transformation rules using Jacobian operations.
Step 1: Define the Hessian Matrix for \(F\)
The Hessian matrix of \(F(a, b, \beta, x)\) with respect to \((a, b, \beta)\) is: \[ \mathbf{H}_F = \begin{bmatrix} \frac{\partial^2 F}{\partial a^2} & \frac{\partial^2 F}{\partial a \partial b} & \frac{\partial^2 F}{\partial a \partial \beta} \\ \frac{\partial^2 F}{\partial b \partial a} & \frac{\partial^2 F}{\partial b^2} & \frac{\partial^2 F}{\partial b \partial \beta} \\ \frac{\partial^2 F}{\partial \beta \partial a} & \frac{\partial^2 F}{\partial \beta \partial b} & \frac{\partial^2 F}{\partial \beta^2} \end{bmatrix}. \]
Using the expressions for second partial derivatives derived earlier: \[ \begin{aligned} \frac{\partial^2 F}{\partial a^2} &= f''(a + \beta x), \quad \frac{\partial^2 F}{\partial b^2} = -f''(b + \beta x), \quad \frac{\partial^2 F}{\partial \beta^2} = x^2 \big(f''(a + \beta x) - f''(b + \beta x)\big), \\ \frac{\partial^2 F}{\partial a \partial b} &= 0, \quad \frac{\partial^2 F}{\partial a \partial \beta} = x f''(a + \beta x), \quad \frac{\partial^2 F}{\partial b \partial \beta} = -x f''(b + \beta x). \end{aligned} \]
Thus: \[ \mathbf{H}_F = \begin{bmatrix} f''(a + \beta x) & 0 & x f''(a + \beta x) \\ 0 & -f''(b + \beta x) & -x f''(b + \beta x) \\ x f''(a + \beta x) & -x f''(b + \beta x) & x^2 \big(f''(a + \beta x) - f''(b + \beta x)\big) \end{bmatrix}. \]
Step 2: Define the Transformation for \(g = \log(F)\)
We apply the chain rule: \[ g = \log(F) \implies \frac{\partial g}{\partial z} = \frac{1}{F} \frac{\partial F}{\partial z}, \] \[ \frac{\partial^2 g}{\partial z \partial w} = \frac{1}{F} \frac{\partial^2 F}{\partial z \partial w} - \frac{1}{F^2} \frac{\partial F}{\partial z} \frac{\partial F}{\partial w}. \]
This can be written compactly in matrix form.
Step 3: Matrix Transformation
Let:
- \(\nabla F = \begin{bmatrix} \frac{\partial F}{\partial a} & \frac{\partial F}{\partial b} & \frac{\partial F}{\partial \beta} \end{bmatrix}^\top\)
- \(\mathbf{H}_F\) be the Hessian matrix of \(F\)
- \(F\) be the scalar value of \(F(a, b, \beta, x)\).
The Hessian of \(g(a, b, \beta, x)\) is given by: \[ \mathbf{H}_g = \frac{1}{F} \mathbf{H}_F - \frac{1}{F^2} \nabla F \nabla F^\top. \]
Explanation:
- \(\frac{1}{F} \mathbf{H}_F\): Scales the Hessian of \(F\) by \(\frac{1}{F}\)
- \(\frac{1}{F^2} \nabla F \nabla F^\top\): Accounts for the interaction of first derivatives of \(F\)
Step 4: Components of \(\nabla F\)
From earlier: \[ \frac{\partial F}{\partial a} = f'(a + \beta x), \quad \frac{\partial F}{\partial b} = -f'(b + \beta x), \quad \frac{\partial F}{\partial \beta} = x \big(f'(a + \beta x) - f'(b + \beta x)\big). \]
Thus: \[ \nabla F = \begin{bmatrix} f'(a + \beta x) \\ -f'(b + \beta x) \\ x \big(f'(a + \beta x) - f'(b + \beta x)\big) \end{bmatrix}. \]
Step 5: Compute \(\nabla F \nabla F^\top\)
The outer product \(\nabla F \nabla F^\top\) is: \[ \nabla F \nabla F^\top = \begin{bmatrix} f'(a + \beta x)^2 & -f'(a + \beta x) f'(b + \beta x) & f'(a + \beta x) x \big(f'(a + \beta x) - f'(b + \beta x)\big) \\ -f'(a + \beta x) f'(b + \beta x) & f'(b + \beta x)^2 & -f'(b + \beta x) x \big(f'(a + \beta x) - f'(b + \beta x)\big) \\ f'(a + \beta x) x \big(f'(a + \beta x) - f'(b + \beta x)\big) & -f'(b + \beta x) x \big(f'(a + \beta x) - f'(b + \beta x)\big) & x^2 \big(f'(a + \beta x) - f'(b + \beta x)\big)^2 \end{bmatrix}. \]
Final Hessian of \(g\)
The Hessian of \(g(a, b, \beta, x)\) is: \[ \mathbf{H}_g = \frac{1}{F} \mathbf{H}_F - \frac{1}{F^2} \nabla F \nabla F^\top. \]
Substitute \(\mathbf{H}_F\) and \(\nabla F \nabla F^\top\) explicitly to get the full matrix. This provides the second derivatives of \(g\) in terms of \(F\), its derivatives, and the structure of \(f\).
Check Speed of NR, nlminb, and glm.fit
glm.fit is tailored to be efficient when Y is binary and there is no penalization, by using iteratively weighted least squares. How does it stack up against NR and nlminb? Let’s try fitting a large binary logistic model.
set.seed(1)
n <- 100000; p <- 100
X <- matrix(rnorm(n * p), nrow=n)
y <- sample(0 : 1, n, TRUE)
tim(NR = lrm.fit(X, y, compstats=FALSE, compvar=FALSE),
nlminb = lrm.fit(X, y, opt_method='nlminb', compstats=FALSE, compvar=FALSE),
glm.fit = glm.fit(cbind(1, X), y), reps=3)Per-run execution time in seconds, averaged over 3 runs
NR nlminb glm.fit
1.415000 1.340333 1.643667 # transx=TRUE adds 2.3s to lrm.fitCheck Convergence Under Complete Separation
Consider a simple example where there is complete separation because the predictor values are identical to the response. In this case the MLE of the intercept is \(-\infty\) and the MLE of the slope is \(\infty\). The MLEs are approximated by \(\alpha=-50, \beta=100\), yielding predicted logits of \(-50\) and \(50\) because the \(\text{expit}\)s are sufficiently close to 0.0 and 1.0.
plogis(-50, log=TRUE)[1] -50plogis( 50, log=TRUE)[1] -1.92875e-22exp(plogis(-50, log=TRUE))[1] 1.92875e-22exp(plogis( 50, log=TRUE))[1] 1See how 4 optimization algorithms fare with their default parameters and with some adjustments. In some of the trace output, the first floating point number listed is -2LL, and following that are the current \(\alpha, \beta\) estimates.
set.seed(1)
x <- sample(0 : 1, 20, TRUE)
y <- x
w <- try(lrm.fit(x, y, opt_method='NR', trace=1)) # default opt_methodIteration:1 -2LL:26.92047 Max |gradient|:9.6 Max |change in parameters|:4.166667
Iteration:2 -2LL:4.704224 Max |gradient|:1.754066 Max |change in parameters|:2.249045
Iteration:3 -2LL:1.588994 Max |gradient|:0.616103 Max |change in parameters|:2.08089
Iteration:4 -2LL:0.5685801 Max |gradient|:0.2233137 Max |change in parameters|:2.028578
Iteration:5 -2LL:0.2071309 Max |gradient|:0.0817248 Max |change in parameters|:2.010364
Iteration:6 -2LL:0.07592908 Max |gradient|:0.03000809 Max |change in parameters|:2.003793
Iteration:7 -2LL:0.02789647 Max |gradient|:0.01103173 Max |change in parameters|:2.001393
Iteration:8 -2LL:0.01025764 Max |gradient|:0.004057316 Max |change in parameters|:2.000512
Iteration:9 -2LL:0.003772913 Max |gradient|:0.001492464 Max |change in parameters|:2.000188
Iteration:10 -2LL:0.001387888 Max |gradient|:0.000549028 Max |change in parameters|:2.000069
Iteration:11 -2LL:0.0005105632 Max |gradient|:0.0002019736 Max |change in parameters|:2.000025w <- try(lrm.fit(x, y, opt_method='nlminb', trace=1)) 0: 26.920467: -0.405465 0.00000
1: 5.9001181: -1.83776 3.67925
2: 1.9469377: -2.99693 5.99700
3: 0.69222129: -4.04687 8.09673
4: 0.25163200: -5.06435 10.1316
5: 0.092171572: -6.07067 12.1442
6: 0.033854569: -7.07298 14.1489
7: 0.012447190: -8.07383 16.1506
8: 0.0045780905: -9.07414 18.1512
9: 0.0016840535: -10.0743 20.1514
10: 0.00061951084: -11.0743 22.1515
11: 0.00022790289: -12.0743 24.1515
12: 8.3840460e-05: -13.0743 26.1515
13: 3.0843137e-05: -14.0743 28.1515
14: 1.1346550e-05: -15.0743 30.1515
15: 4.1741617e-06: -16.0743 32.1515
16: 1.5355882e-06: -17.0743 34.1515
17: 5.6491130e-07: -18.0743 36.1515
18: 2.0781925e-07: -19.0743 38.1515
19: 7.6452432e-08: -20.0743 40.1515
20: 2.8125276e-08: -21.0743 42.1515
21: 1.0346714e-08: -22.0743 44.1515
22: 3.8063437e-09: -23.0743 46.1515
23: 1.4002772e-09: -24.0743 48.1515
24: 5.1513283e-10: -25.0743 50.1515
25: 1.8950352e-10: -26.0743 52.1515
26: 6.9714901e-11: -27.0743 54.1515
27: 2.5648816e-11: -28.0743 56.1515
28: 9.4360075e-12: -29.0743 58.1515
29: 3.4692249e-12: -30.0743 60.1515
30: 1.2789769e-12: -31.0743 62.1515
31: 4.7073456e-13: -32.0743 64.1515
32: 1.6875390e-13: -33.0743 66.1515
33: 6.2172489e-14: -34.0743 68.1515
34: 2.6645353e-14: -35.0743 70.1515
35: 8.8817842e-15: -36.0743 72.1515
36: 0.0000000: -37.0743 74.1515
37: 0.0000000: -37.0743 74.1515
Error in chol.default(info) :
the leading minor of order 1 is not positive
Error in chol.default(info) :
the leading minor of order 1 is not positivew <- try(lrm.fit(x, y, opt_method='glm.fit', trace=1))Deviance = 3.368709 Iterations - 1
Deviance = 1.16701 Iterations - 2
Deviance = 0.4207147 Iterations - 3
Deviance = 0.1536571 Iterations - 4
Deviance = 0.0563787 Iterations - 5
Deviance = 0.02072057 Iterations - 6
Deviance = 0.007619969 Iterations - 7
Deviance = 0.002802865 Iterations - 8
Deviance = 0.001031067 Iterations - 9
Deviance = 0.0003793016 Iterations - 10
Deviance = 0.0001395364 Iterations - 11
Deviance = 5.133244e-05 Iterations - 12
Deviance = 1.888413e-05 Iterations - 13
Deviance = 6.947082e-06 Iterations - 14
Deviance = 2.555688e-06 Iterations - 15
Deviance = 9.401851e-07 Iterations - 16
Deviance = 3.458748e-07 Iterations - 17
Deviance = 1.272402e-07 Iterations - 18
Deviance = 4.680906e-08 Iterations - 19
Deviance = 1.722009e-08 Iterations - 20
Deviance = 6.33492e-09 Iterations - 21
Deviance = 2.330491e-09 Iterations - 22
Deviance = 8.573409e-10 Iterations - 23
Deviance = 3.15401e-10 Iterations - 24
Deviance = 1.160316e-10 Iterations - 25
Deviance = 4.268585e-11 Iterations - 26
Deviance = 1.570299e-11 Iterations - 27
Deviance = 5.782042e-12 Iterations - 28w <- try(lrm.fit(x, y, opt_method='BFGS', trace=1))initial value 26.920467
iter 10 value 0.000153
iter 20 value 0.000017
iter 30 value 0.000004
iter 40 value 0.000001
iter 50 value 0.000000
final value 0.000000
stopped after 50 iterationsnlminbtook 37 iterations, going so far that the Hessian matrix was singular. It should have stopped with 10.glm.fittook 28 iterations; should have stopped with 10BFGS: stopped after 50 iterations; should have stopped with 10
Now specify arguments to lrm.fit that are tuned to this task.
w <- lrm.fit(x, y, opt_method='nlminb', abstol=1e-3, trace=1) 0: 26.920467: -0.405465 0.00000
1: 5.9001181: -1.83776 3.67925
2: 1.9469377: -2.99693 5.99700
3: 0.69222129: -4.04687 8.09673
4: 0.25163200: -5.06435 10.1316
5: 0.092171572: -6.07067 12.1442
6: 0.033854569: -7.07298 14.1489
7: 0.012447190: -8.07383 16.1506
8: 0.0045780905: -9.07414 18.1512
9: 0.0016840535: -10.0743 20.1514
10: 0.00061951084: -11.0743 22.1515w <- lrm.fit(x, y, opt_method='glm.fit', reltol=1e-3, trace=1)Deviance = 3.368709 Iterations - 1
Deviance = 1.16701 Iterations - 2
Deviance = 0.4207147 Iterations - 3
Deviance = 0.1536571 Iterations - 4
Deviance = 0.0563787 Iterations - 5
Deviance = 0.02072057 Iterations - 6
Deviance = 0.007619969 Iterations - 7
Deviance = 0.002802865 Iterations - 8
Deviance = 0.001031067 Iterations - 9
Deviance = 0.0003793016 Iterations - 10
Deviance = 0.0001395364 Iterations - 11
Deviance = 5.133244e-05 Iterations - 12w <- lrm.fit(x, y, opt_method='BFGS', reltol=1e-4, trace=1)initial value 26.920467
iter 10 value 0.000153
final value 0.000100
convergedThe tolerance parameters are too large to use when infinite coefficients are not a problem.
Check 4 Algorithms With k=1000
For timings that follow, compstats=FALSE is specified to lrm.fit so that we can focus on computationally efficiencies of various optimization algorithms. Some of the differences in run times may not seem to be consequential, but once extremely large datasets are analyzed or one needs to fit models in a bootstrap or Monte Carlo simulation loop, the differences in speed will matter.
When the number of distinct Y values is large, and this far exceeds the number of predictors (\(k >> p\)), the rms orm function should be used. It takes into account the sparsity of the intercept portion of the Hessian matrix, which is tri-band diagonal and has only \(3\times k\) nonzero values for \(k+1\) distinct Y values. Outside of orm and SAS JMP, ordinal regression fitting software treats the Hessian matrix as being \(k\times k\) and does not capitalize on sparsity.
Note that for Bayesian MCMC this is not an issue as posterior sampling does not need the Hessian.
set.seed(1)
n <- 10000; k <- 1000
x <- rnorm(n); y <- sample(0:k, n, TRUE)
length(unique(y))[1] 1001tim(orm = rms::orm.fit(x, y, eps=1e-10),
bfgs = lrm.fit(x, y, opt_method='BFGS', compvar=FALSE, compstats=FALSE, maxit=100),
nlminb = lrm.fit(x, y, opt_method='nlminb', compstats=FALSE),
nr = lrm.fit(x, y, opt_method='NR', compstats=FALSE),
nlm = lrm.fit(x, y, opt_method='nlm', compstats=FALSE),
polr = MASS::polr(factor(y) ~ x, control=list(reltol=1e-10)),
reps= 2)Per-run execution time in seconds, averaged over 2 runs
orm bfgs nlminb nr nlm polr
0.4905 0.0425 0.6175 0.5180 10.1575 6.4700 smod() deviance max_abs_u iter
orm 137142.5 NA NA
bfgs 137142.5 2.376188e+00 4
nlminb 137142.5 1.431033e-09 3
nr 137142.5 7.625981e-05 2
nlm 137142.5 7.625981e-05 1
polr 137142.5 NA NA
Maximum |difference in coefficients|, Maximum |relative difference|
worst ratio of covariance matrices Comparison Max |difference| Max |rel diff| Cov ratio
1 orm vs. bfgs 6.991343e-06 3.950698e-04
2 orm vs. nlminb 1.213373e-13 1.145216e-13 1.000000
3 orm vs. nr 1.213202e-13 1.139669e-13 1.000000
4 orm vs. nlm 4.136310e-07 3.812141e-07 1.001368
5 orm vs. polr 9.637588e-06 1.359060e-05
6 bfgs vs. nlminb 6.991343e-06 3.950698e-04
7 bfgs vs. nr 6.991343e-06 3.950698e-04
8 bfgs vs. nlm 6.776204e-06 3.949523e-04
9 bfgs vs. polr 9.425718e-06 4.030520e-04
10 nlminb vs. nr 3.307971e-16 9.636021e-16 1.000000
11 nlminb vs. nlm 4.136309e-07 3.812140e-07 1.001368
12 nlminb vs. polr 9.637588e-06 1.359060e-05
13 nr vs. nlm 4.136309e-07 3.812140e-07 1.001368
14 nr vs. polr 9.637588e-06 1.359060e-05
15 nlm vs. polr 9.231301e-06 1.326760e-05 Check Timing and Agreement for n=100000, k=10, p=5
Check timing and calculation agreement for n=100000, 10 intercepts, 5 predictors.
set.seed(1)
n <- 100000
y <- sample(0 : 10, n, TRUE)
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- rnorm(n)
x5 <- rnorm(n)
X <- cbind(x1, x2, x3, x4, x5)
tim(old.lrm.fit = lrm.fit.old(X, y, eps=1e-7),
nr = lrm.fit(X, y, opt_method='NR', compstats=FALSE),
nlm = lrm.fit(X, y, opt_method='nlm', compstats=FALSE),
nlminb = lrm.fit(X, y, opt_method='nlminb', compstats=FALSE, transx=TRUE),
nlminb.notransx = lrm.fit(X, y, opt_method='nlminb', compstats=FALSE, transx=FALSE),
bfgs = lrm.fit(X, y, opt_method='BFGS', compvar=FALSE, compstats=FALSE),
bfgs.reltol = lrm.fit(X, y, opt_method='BFGS', compvar=FALSE,
compstats=FALSE, reltol=1e-12),
polr = MASS::polr(factor(y) ~ X,
control=list(reltol=1e-10)),
reps = 5)Per-run execution time in seconds, averaged over 5 runs
old.lrm.fit nr nlm nlminb nlminb.notransx
0.1806 0.1056 0.5990 0.0944 0.0946
bfgs bfgs.reltol polr
0.4340 0.6882 2.3976 smod() deviance max_abs_u iter
old.lrm.fit 479562.9 8.754331e-12 NA
nr 479562.9 1.992553e-07 3
nlm 479562.9 5.051226e-02 1
nlminb 479562.9 1.992456e-07 3
nlminb.notransx 479562.9 1.992552e-07 3
bfgs 479562.9 6.987317e-01 7
bfgs.reltol 479562.9 3.683979e-05 19
polr 479562.9 NA NA
Maximum |difference in coefficients|, Maximum |relative difference|
worst ratio of covariance matrices Comparison Max |difference| Max |rel diff| Cov ratio
1 old.lrm.fit vs. nr 5.582412e-16 1.286951e-14 1.000000
2 old.lrm.fit vs. nlm 3.004074e-06 2.122140e-05 1.000202
3 old.lrm.fit vs. nlminb 1.053797e-11 4.463604e-11 1.000000
4 old.lrm.fit vs. nlminb.notransx 1.053798e-11 4.462038e-11 1.000000
5 old.lrm.fit vs. bfgs 9.057305e-06 7.174198e-04
6 old.lrm.fit vs. bfgs.reltol 5.712939e-08 1.703834e-06
7 old.lrm.fit vs. polr 5.977469e-06 2.409730e-03
8 nr vs. nlm 3.004074e-06 2.122140e-05 1.000202
9 nr vs. nlminb 1.053798e-11 4.462471e-11 1.000000
10 nr vs. nlminb.notransx 1.053798e-11 4.460905e-11 1.000000
11 nr vs. bfgs 9.057305e-06 7.174198e-04
12 nr vs. bfgs.reltol 5.712939e-08 1.703834e-06
13 nr vs. polr 5.977469e-06 2.409730e-03
14 nlm vs. nlminb 3.004063e-06 2.122136e-05 1.000202
15 nlm vs. nlminb.notransx 3.004063e-06 2.122136e-05 1.000202
16 nlm vs. bfgs 8.867603e-06 7.344671e-04
17 nlm vs. bfgs.reltol 3.059332e-06 2.243215e-05
18 nlm vs. polr 7.995997e-06 2.398944e-03
19 nlminb vs. nlminb.notransx 2.695688e-17 2.221290e-14 1.000000
20 nlminb vs. bfgs 9.057301e-06 7.174198e-04
21 nlminb vs. bfgs.reltol 5.713989e-08 1.703866e-06
22 nlminb vs. polr 5.977476e-06 2.409730e-03
23 nlminb.notransx vs. bfgs 9.057301e-06 7.174198e-04
24 nlminb.notransx vs. bfgs.reltol 5.713989e-08 1.703866e-06
25 nlminb.notransx vs. polr 5.977476e-06 2.409730e-03
26 bfgs vs. bfgs.reltol 9.069540e-06 7.167658e-04
27 bfgs vs. polr 1.347117e-05 2.800575e-03
28 bfgs.reltol vs. polr 5.951212e-06 2.410693e-03 Other Speed Tests
n=1,000,000, p=100 predictors, k=50 intercepts
lrm.fit: 14.9s (14.4 withopt_method=nlminb, 150s withopt_method='BFGS')orm.fit: 95sMASS::polr: 70s
Check Impact of initglm and transx
Generate a sample of 500 with 30 predictors and 269 levels of Y where a subset of the predictors are strongly related to Y and there are collinearities.
set.seed(1)
n <- 500
p <- 30
x <- matrix(runif(n * p), nrow=n)
x[, 1:8] <- x[, 1:8] + 2 * x[, 9]
s <- varclus(~ x)$hclust
plot(as.dendrogram(s), horiz=TRUE, axes=FALSE,
xlab=expression(paste('Spearman ', rho^2)))
rh <- seq(0, 1, by=0.1)
axis(1, at=1 - rh, labels=format(rh))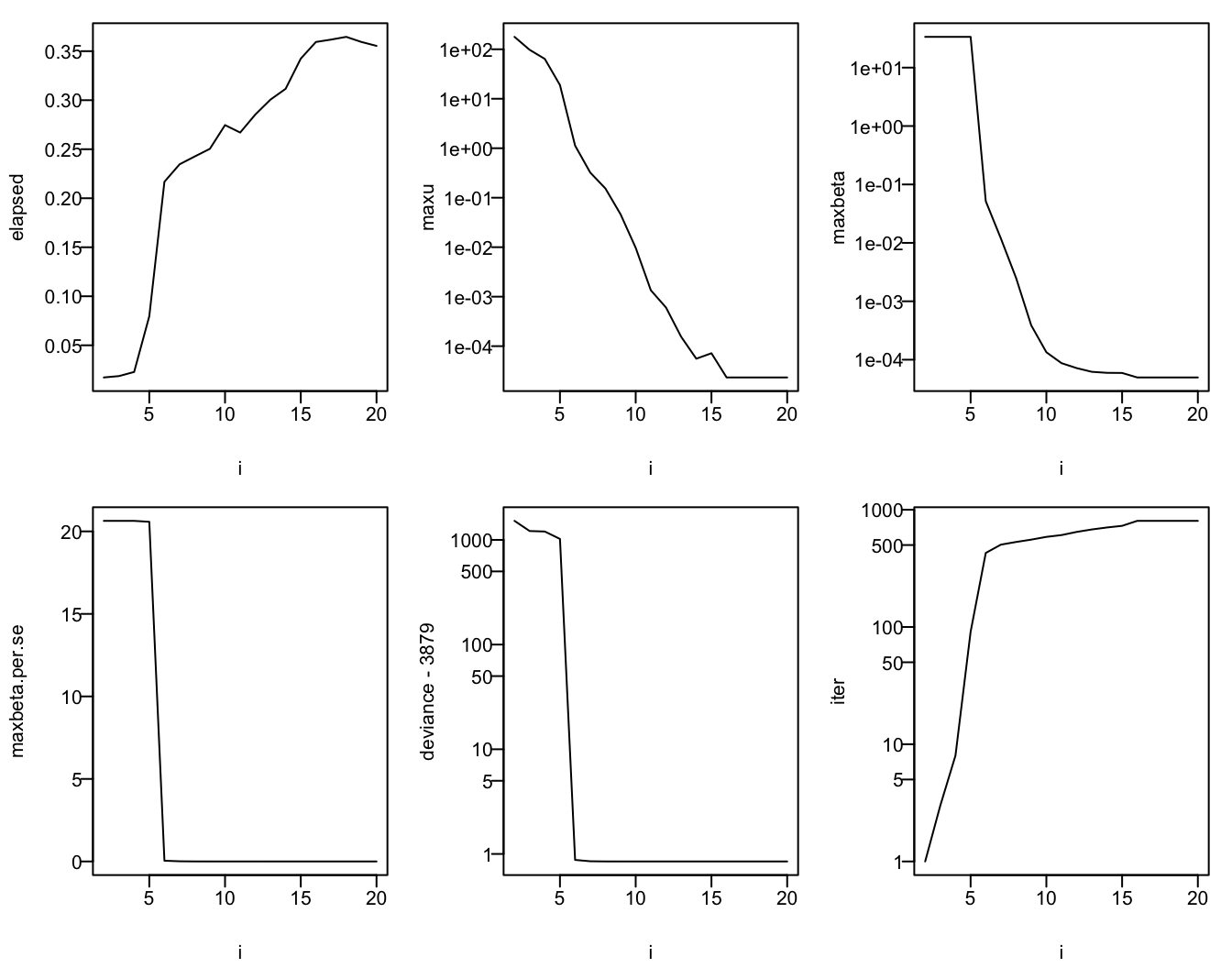
y <- x[, 1] + 2 * x[, 2] + 3 * x[, 3] + 4 * x[, 4]+ 5 * x[, 5] +
3 * runif(n, -1, 1)
y <- round(y, 1)
length(unique(y))[1] 269f <- function(..., opt_method='NR')
lrm.fit(x, y, compstats=FALSE, opt_method=opt_method, maxit=1000, ...)
# f(initglm=TRUE) (using nlminb) would not work: NA/NaN gradient evaluation
# This did not happen without collinearities
tim(default = f(),
transx = f(transx=TRUE),
nlm = f(opt_method='nlm'),
bfgs = f(opt_method='BFGS'),
nlminb = f(opt_method='NR'),
reps = 10 )Per-run execution time in seconds, averaged over 10 runs
default transx nlm bfgs nlminb
0.0382 0.0588 0.4163 0.2819 0.0380 smod() deviance max_abs_u iter
default 3879.848 6.112532e-05 7
transx 3879.848 6.112532e-05 7
nlm 3879.848 6.112532e-05 6
bfgs 3879.848 9.721526e-03 587
nlminb 3879.848 6.112532e-05 7
Maximum |difference in coefficients|, Maximum |relative difference|
worst ratio of covariance matrices Comparison Max |difference| Max |rel diff| Cov ratio
1 default vs. transx 3.545735e-14 2.931589e-15 1.000000
2 default vs. nlm 1.063035e-05 5.990158e-07 1.000291
3 default vs. bfgs 1.918945e-05 3.544624e-06
4 default vs. nlminb 0.000000e+00 0.000000e+00 1.000000
5 transx vs. nlm 1.063035e-05 5.990158e-07 1.000291
6 transx vs. bfgs 1.918945e-05 3.544624e-06
7 transx vs. nlminb 3.545735e-14 2.931589e-15 1.000000
8 nlm vs. bfgs 2.249980e-05 3.725436e-06
9 nlm vs. nlminb 1.063035e-05 5.990158e-07 1.000291
10 bfgs vs. nlminb 1.918945e-05 3.544624e-06 Break-even Point for lrm.fit vs. orm.fit
The fitting function for rms::orm, orm.fit, uses sparse Hessian matrices so that the computation time is roughly proportional to \(n (3k + p^{2} + kp)\) where \(k\) is the number of intercepts and \(p\) is the number of predictors. Computation of the Hessian in lrm.fit needs about \(n (k + p)^{2}\) computations, but some parts of the computation are faster and there is some overhead of handling sparse matrices in orm.fit. Let’s explore execution time as a function of \(k\) when \(n=10000, p=30\) and \(k\) varies.
if(! file.exists('breakeven.rds')) {
set.seed(1)
n <- 10000
p <- 30
ks <- seq(500, 3500, by=500)
l <- length(ks)
t1 <- t2 <- d <- numeric(l)
x <- matrix(rnorm(n * p), nrow=n)
for(i in 1 : l) {
cat(ks[i], ' ')
y <- rep(0 : ks[i], length=n)
t1[i] <- system.time(f <- rms::lrm.fit(x, y))['elapsed']
t2[i] <- system.time(g <- rms::orm.fit(x, y))['elapsed']
d [i] <- m(coef(f) - coef(g))
}
w <- llist(ks, t1, t2, d)
saveRDS(w, 'breakeven.rds')
} else {
w <- readRDS('breakeven.rds')
ks <- w$ks; t1 <- w$t1; t2 <- w$t2; d <- w$d
}
# Make sure coefficients agree
range(d)[1] 8.881784e-15 1.687539e-13plot(ks, t1, type='b', xlab='k', ylab='Time, seconds')
points(ks, t2, col='red')
lines (ks, t2, col='red')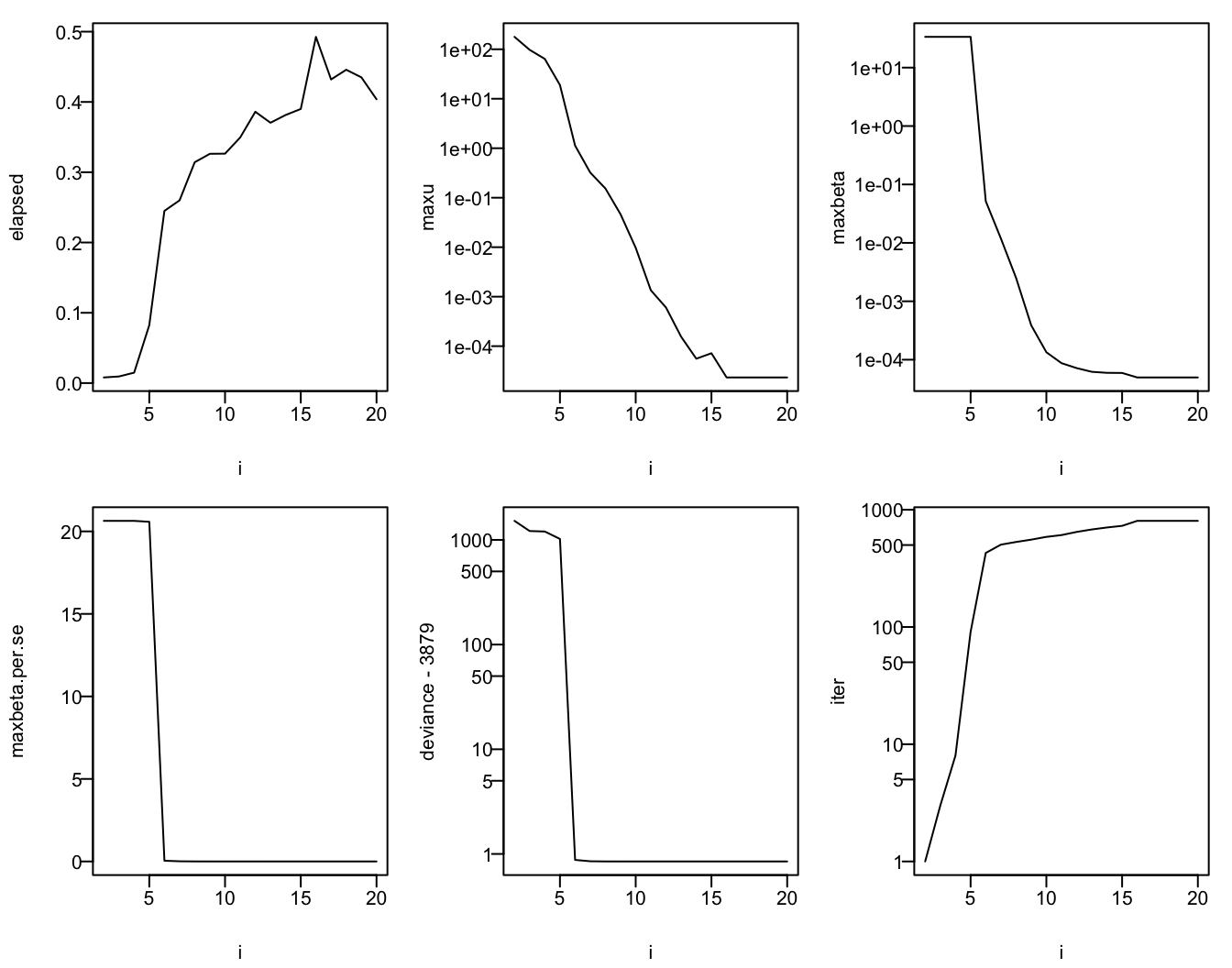
Execution time for orm.fit is linear in \(k\) but is quadratic for lrm.fit. The breakeven point is around \(k=2500\) intercepts. Even for lower \(k\) there is an advantage to the sparse matrix approach: the lower storage space and downstream computation time for anova, etc. The \(3530\times 3530\) covariance matrix for the highest \(k=3500\) is 100MB from lrm.fit. orm.fit stores a covariance matrix that is only for the median intercept, and this takes 12KB. It stores the full sparse information matrix that includes all intercepts, requiring 2.7MB. The vcov method for orm computes needed portions of the covariance matrix on demand.
To stay under an R object size for the covariance matrix of 2MB one can analyze up to 500 distinct ordinal Y values with
lrm.fit.Better Understanding Convergence with BFGS Optimizer
Using the same simulated data just used, use BFGS to fit an ordinal model with relative tolerance varying from \(10^{-2}\) to \(10^{-20}\). Estimates are compared to orm. In addition to comparing parameter estimates as done above we also compute differences in units of standard errors as computed by orm.
g <- rms::orm(y ~ x, eps=1e-10)
se <- sqrt(diag(vcov(g, intercepts='all')))
d <- NULL
for(i in 2 : 20) {
s <- system.time(for(j in 1:5)
f <- lrm.fit(x, y, compstats=FALSE,
opt_method='BFGS',
maxit=1000,
reltol=10^(-i)))['elapsed']
w <- data.frame(i, elapsed=s / 5, maxu=m(f$u),
maxbeta=m(coef(g) - coef(f)),
maxbeta.per.se=m((coef(g) - coef(f))/se),
deviance=tail(f$deviance, 1),
iter=tail(f$iter, 1))
d <- rbind(d, w)
}
rownames(d) <- NULL
d i elapsed maxu maxbeta maxbeta.per.se deviance iter
1 2 0.0082 1.781729e+02 3.361068e+01 2.063781e+01 5399.000 1
2 3 0.0098 9.738995e+01 3.361066e+01 2.063722e+01 5094.243 3
3 4 0.0142 6.384426e+01 3.361066e+01 2.063699e+01 5081.404 8
4 5 0.0862 1.892680e+01 3.360747e+01 2.058161e+01 4900.327 91
5 6 0.2560 1.128232e+00 5.167229e-02 4.465468e-02 3879.877 428
6 7 0.3204 3.220871e-01 1.185453e-02 1.024456e-02 3879.851 504
7 8 0.2732 1.538043e-01 2.510429e-03 1.842095e-03 3879.848 531
8 9 0.3364 4.632918e-02 3.877973e-04 3.351305e-04 3879.848 556
9 10 0.3906 9.721526e-03 1.342389e-04 1.055845e-04 3879.848 587
10 11 0.3200 1.345625e-03 8.725462e-05 6.402546e-05 3879.848 608
11 12 0.3566 6.036158e-04 7.179465e-05 4.097949e-05 3879.848 647
12 13 0.3672 1.547283e-04 6.205067e-05 3.721365e-05 3879.848 679
13 14 0.4282 5.574421e-05 5.959543e-05 3.619120e-05 3879.848 706
14 15 0.3752 7.187127e-05 5.930900e-05 3.584911e-05 3879.848 729
15 16 0.4546 2.330094e-05 4.968143e-05 2.996054e-05 3879.848 804
16 17 0.4860 2.330094e-05 4.968143e-05 2.996054e-05 3879.848 804
17 18 0.4580 2.330094e-05 4.968143e-05 2.996054e-05 3879.848 804
18 19 0.4340 2.330094e-05 4.968143e-05 2.996054e-05 3879.848 804
19 20 0.4236 2.330094e-05 4.968143e-05 2.996054e-05 3879.848 804z <- c(deviance=8, beta=10, beta.se=6, grad=15) # minimum i for which success achieved
h <- function() abline(v=z, col=gray(0.60))
h <- function() {} # remove this line to show reference lines
par(mfrow=c(2, 3), mar=c(4, 4, 1, 1), las=1, mgp=c(2.8, .45, 0))
with(d, {
plot(i, elapsed, type='l'); h()
plot(i, maxu, type='l', log='y'); h()
plot(i, maxbeta, type='l', log='y'); h()
plot(i, maxbeta.per.se, type='l'); h()
plot(i, deviance - 3879, type='l', log='y'); h()
plot(i, iter, type='l', log='y'); h()
})
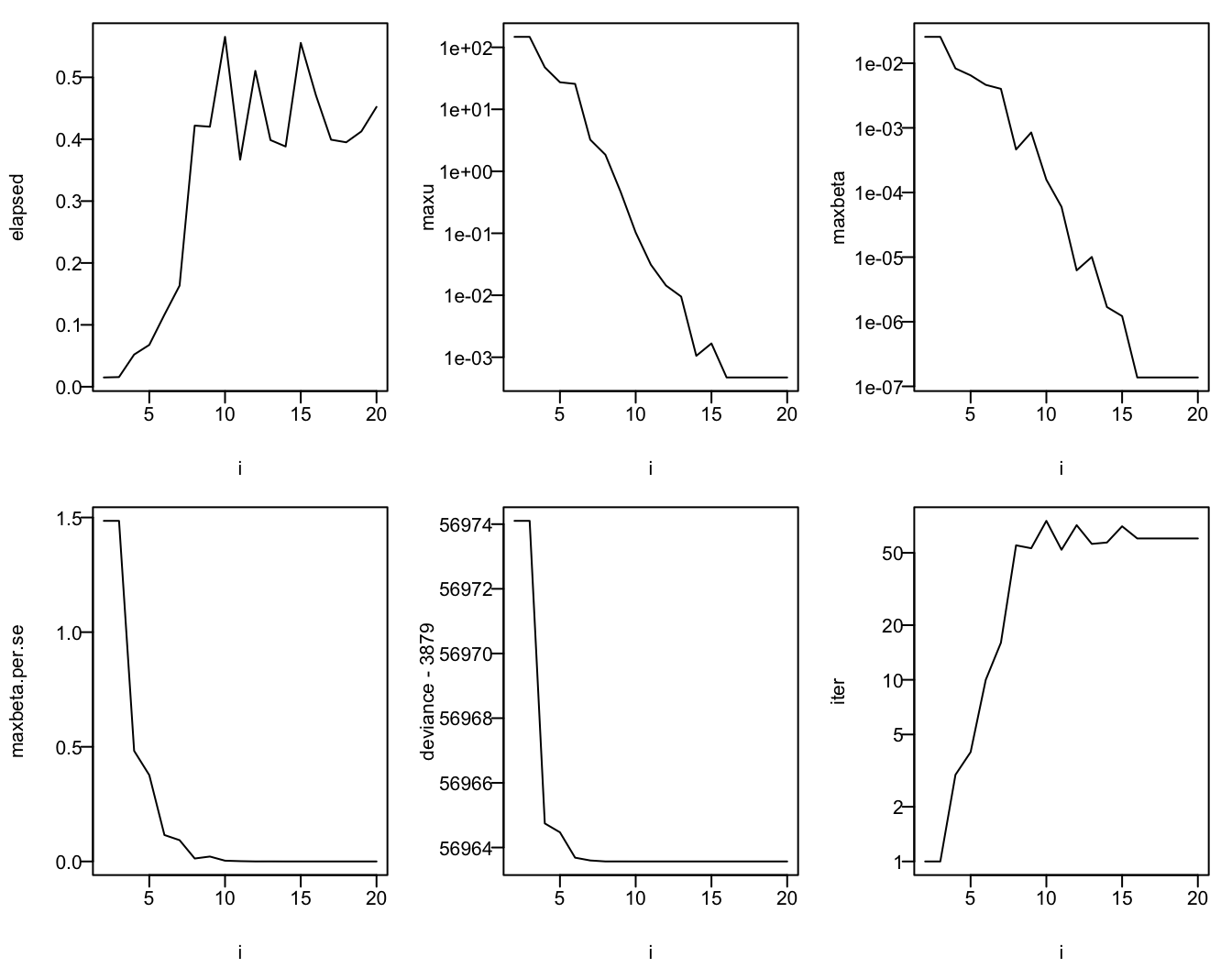
NULLSee that stochastic convergence, as judged by deviance, occurs by the time the relative tolerance is \(10^{-8}\), by \(10^{-10}\) to control maximum absolute parameter difference, by \(10^{-6}\) to get parameter estimates to within 0.06 standard error, and by \(10^{-15}\) to achieve gradients \(< 10^{-4}\) in absolute value.
When using BFGS a recommendation is to use a relative tolerance of \(10^{-8}\) to nail down estimates to the extent that it matters precision-wise, and use \(10^{-10}\) to achieve reproducibility.
Recall that BFGS is only appealing when the number of intercepts is large, you don’t need the covariance matrix, and you are not using orm.
Matrix Inversion
The information matrix (negative Hessian) must be inverted to compute the variance-covariance matrix. The default inversion method in R is the solve function, which defaults to using the LU decomposition. This is a fast algorithm, but the Cholesky decomposition is faster and behaves as well as LU numerically. Another approach uses the QR decomposition, implemented in the qr.solve function. Let’s compare speed and accuracy of the three approaches when applied to a high-dimensional almost-singular matrix.
# ChatGPT created this function to generate an almost-singular symmetric
# positive definite matrix of dimension p x p
genas <- function(p, epsilon = 1e-8) {
# Generate a random symmetric positive definite matrix
A <- matrix(rnorm(p^2), p, p)
A <- A + t(A) + p * diag(p) # Symmetric and positive definite
# Modify eigenvalues to make the matrix almost singular
eigen_decomp <- eigen(A)
eigen_decomp$values[p] <- epsilon # Set the smallest eigenvalue close to zero
eigen_decomp$vectors %*% diag(eigen_decomp$values) %*% t(eigen_decomp$vectors)
}
set.seed(3)
x <- genas(750, 1e-9)
x[1:3, 1:3] [,1] [,2] [,3]
[1,] 748.051108 -1.0242634 0.3929600
[2,] -1.024263 747.2599805 0.9261079
[3,] 0.392960 0.9261079 745.6809913# LU method
system.time(for(i in 1:3) a <- solve(x)) user system elapsed
0.633 0.010 0.643 mad(x, solve(a)) # reverse the inversion and compare to x mad relmad
0.0001921486 0.0006909615 m(diag(750) - x %*% a) # compare x inverse * x to identity matrix[1] 3.083591e-05# QR
system.time(for(i in 1:3) b <- qr.solve(x, tol=1e-13)) user system elapsed
1.481 0.023 1.504 mad(x, qr.solve(b, tol=1e-13)) mad relmad
0.0002050283 0.0007250491 m(diag(750) - x %*% b)[1] 3.917762e-05# Cholesky
system.time(for(i in 1:3) ch <- chol2inv(chol(x))) user system elapsed
0.323 0.005 0.329 mad(x, chol2inv(chol(ch))) # mean |difference| and mean relative difference mad relmad
0.0002323721 0.0008362380 m(diag(750) - x %*% ch) # mean |difference|[1] 1.71175e-05QR takes significantly longer and offers no accuracy advantange. Inversion via Cholesky decomposition was almost twice as fast as LU, though both methods took less than \(\frac{1}{4}\) of a second to invert a \(750\times 750\) matrix. Cholesky was a little more accurate in getting the product of the original matrix and its inverse closer to an identity matrix. Cholesky was very slightly worse in recovering the original matrix by inverting its inverse.
lrm.fit uses Cholesky when inverting the final Hessian matrix. During Newton-Raphson updating when opt_method='NR', it uses solve (LU method) because it is more accurate to let solve multiply the inverse Hessian by the gradient vector in one step.
Other Resources
- Video by Richad McElreath explaining numerical accuracy issues in log likelihood calculations.
- R CRAN Task Views on optimizers
- Vignettes by John Nash et al.
- R
ucminfpackage - R
nloptrpackage - R code:
lrmandlrm.fit - Fortran code:
lrmll
Computing Environment
grateful::cite_packages(pkgs='Session', output='paragraph', out.dir='.',
cite.tidyverse=FALSE, omit=c('grateful', 'ggplot2'))We used R version 4.4.0 (R Core Team 2024) and the following R packages: Hmisc v. 5.2.1 (Harrell Jr 2024a), tlrm v. 0.0.1 (Harrell Jr 2024b).
The code was run on macOS Sonoma 14.7.1 on a Macbook Pro M2 Max, running on a single core.
References
Harrell Jr, Frank E. 2024a. Hmisc: Harrell Miscellaneous. https://hbiostat.org/R/Hmisc/.
———. 2024b. tlrm: Test Package.
R Core Team. 2024. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.